Home | Archives | About | Login | Submissions | Notify | Contact | Search

ES Home > Vol. 6, No. 1 > Art. 16 Copyright © 2002 by the author(s). Published here under license by The Resilience Alliance. Go to the pdf version of this article. The following is the established format for referencing this article: Brook, B. W., D. W. Tonkyn, J. J. O'Grady, and R. Frankham. 2002. Contribution of inbreeding to extinction risk in threatened species. Conservation Ecology 6(1): 16. [online] URL: http://www.consecol.org/vol6/iss1/art16/ A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link. Report Contribution of Inbreeding to Extinction Risk in Threatened Species Barry W. Brook1, David W. Tonkyn2, Julian J. O'Grady3, and Richard Frankham3 1Northern Territory University; 2Clemson University; 3Macquarie University Abstract Introduction Methods Population viability analyses Statistical analyses Results Projected population sizes and extinction risk Differences in median times to extinction due to inbreeding depression Comparisons among taxa with regard to the impact of inbreeding depression Relationship between impact of inbreeding and population growth rate Discussion Responses to this Article Acknowledgments Literature Cited ABSTRACT Wild populations face threats both from deterministic factors, e.g., habitat loss, overexploitation, pollution, and introduced species, and from stochastic events of a demographic, genetic, and environmental nature, including catastrophes. Inbreeding reduces reproductive fitness in naturally outbreeding species, but its role in extinctions of wild populations is controversial. To evaluate critically the role of inbreeding in extinction, we conducted realistic population viability analyses of 20 threatened species, with and without inbreeding depression, using initial population sizes of 50, 250, and 1000. Inbreeding markedly decreased median times to extinction by 28.5, 30.5, and 25% for initial populations of 50, 250, and 1000, respectively, and the impacts were similar across major taxa. The major variable explaining differences among species was initial population growth rate, whereas the impact of inbreeding was least in species with negative growth rates. These results demonstrate that the prospects for survival of threatened species will usually be seriously overestimated if genetic factors are disregarded, and that inappropriate recovery plans may be instituted if inbreeding depression is ignored. KEY WORDS: endangered species, inbreeding depression, life histories, median time to extinction, population viability analysis, purging. Published: June 27, 2002 INTRODUCTION Species in natural habitats face threats both from deterministic factors such as habitat loss, overexploitation, pollution, and introduced species, and from stochastic events associated with small population size; such events may be of a demographic, genetic, or environmental nature, including catastrophes (World Conservation Monitoring Centre 1992). Genetic stochasticity encompasses inbreeding depression, loss of genetic diversity, and mutational accumulation (Frankham et al. 2002). Inbreeding is the most immediate and potentially damaging of these (Frankham 1995a). Essentially, all well-studied naturally outbreeding species show depressed reproductive fitness in inbred individuals; this phenomenon is known as inbreeding depression (Falconer and Mackay 1996, Lynch and Walsh 1998, Hedrick and Kalinowski 2000). This has been demonstrated in the laboratory (see Frankham 1995b), in zoos (Ralls et al. 1988), and in the wild (see Crnokrak and Roff 1999). Although some scientists have been skeptical about the occurrence of inbreeding depression in wild populations, compelling evidence for it now exists. Of 157 valid data sets across 34 taxa reviewed by Crnokrak and Roff (1999), 90% showed differences indicating that inbreeding was deleterious to reproductive fitness (Frankham 2000). There is controversy about the contribution of inbreeding depression to the extinction risk for populations in nature. Whereas it is generally acknowledged that any depressive effect on survival, such as inbreeding, will tend to reduce population growth rates, it is not generally accepted that inbreeding itself translates into elevated extinction risks. For instance, Lande (1988) and others (e.g., Caro and Laurenson 1994, Caughley 1994, Dobson 1999) have argued that inbreeding plays an extremely minor role in extinctions, because demographic and environmental stochasticity, as well as catastrophes, will drive small populations to extinction before genetic factors become important. Although Lande (1995) now believes that genetic factors do contribute to extinction, he is referring to accumulations of new deleterious mutations rather than to inbreeding depression. However, inbreeding depression has been linked to population declines and extinctions in both captivity (Frankham 1995b) and the wild (Vrijenhoek 1994, Newman and Pilson 1997, Saccheri et al. 1998, Westemeier et al. 1998, Madsen et al. 1999). All these studies discussed individual cases, but none provided comprehensive evidence covering a wide range of threatened species or gave a clear indication of when inbreeding is important and when it is not. Levels of inbreeding (F) are inversely related to effective population size (Ne) and increase with generations (t), as follows (Falconer and Mackay 1996): F = 1 - (1 - 1/[2 Ne])t ~ 1 - e-t/[2Ne] (1) Reductions in fecundity and survival are related to F (Falconer and Mackay 1996, Lynch and Walsh 1998). Consequently, inbreeding is expected to have its greatest impact when populations are small and the number of generations is large. The effects of other stochastic factors are also expected to show similar patterns. The magnitude of inbreeding depression may be reduced by selective purging of recessive deleterious alleles by natural selection, although the relative importance of purging is also controversial (see Byers and Waller 1999, Miller and Hedrick 2001). Furthermore, there is still some disagreement with regard to the differential effects of purging in very small vs. large populations (Frankham et al. 2001). Purging has little impact in very small populations, e.g., with regular selfing or full-sib mating, but has clear effects in moderate to large populations (D. H. Reed, D. A. Briscoe, and R. Frankham, unpublished data). Interactions are expected between the impacts of inbreeding and both deterministic factors and "nongenetic" stochastic factors. Human-associated threats such as habitat loss, overexploitation, pollution, and introduced species (World Conservation Monitoring Centre 1992) reduce population sizes and increase inbreeding, which in turn reduces individual survival and fecundity and therefore population sizes, creating the potential for an extinction "vortex" (Gilpin and Soulé 1986). Fluctuations in population size resulting from demographic and environmental stochasticity and catastrophes reduce Ne, increase F, and therefore increase the risk of extinction (van Noordwijk 1994, Tanaka 2000). Studies of the effects of inbreeding on extinction risk in natural populations are hampered by difficulties in separating the genetic and nongenetic components. In addition, constraints on time and resources have forced past studies to concentrate on only a few high-profile species. As a result, stochastic computer projections offer the only means of comprehensively investigating the role of inbreeding in extinction. They make it possible to investigate many species, can be performed relatively quickly, and allow for the inclusion or exclusion of inbreeding in concert with demographic and environmental stochasticity and catastrophes; this is impossible in field experiments. Population viability analysis (PVA) is widely used to predict the fate of threatened populations by projecting life histories forward using stochastic computer simulations (see Akçakaya and Sjögren-Gulve 2000, Menges 2000, Beissinger and McCullough 2002). Critically, PVA has been shown to produce unbiased predictions, making it an ideal research tool for this purpose (Brook et al. 2000). Four studies have used PVA to investigate the effects of inbreeding depression on population growth and/or extinction risk (Burgman and Lamont 1992, Dobson et al. 1992, Mills and Smouse 1994, Oostermeijer 2000). However, these studies focused on specific or hypothetical cases, were often projected for only a few generations, and failed to consider the impact of purging. As a result, their overall message was unclear. For example, Burgman and Lamont (1992) found that inbreeding depression had very little impact on the viability of the plant Banksia cuneata, whereas Oostermeijer (2000) found that it had a strong impact on Gentiana pneumonanthe. Dobson et al. (1992) predicted that inbreeding depression would increase the extinction risk of rhinoceros populations and that its impact depended on population size. Mills and Smouse (1994) showed that inbreeding would have an impact on generalized animal life histories, especially those with slow initial population growth. The objective of this study was to determine the contribution of inbreeding to extinction risk for a broad range of threatened taxa. We used realistic PVA models that included the effects of purging to project the population dynamics for 20 actual threatened species covering a range of life history types, both with and without inbreeding depression. We also investigated the impact of different initial population sizes and different population growth rates. METHODS Population viability analyses Realistic population viability analysis (PVA) models were used to project the future population dynamics of 20 threatened species subject to demographic and environmental stochasticity and to catastrophes, with and without inbreeding depression. The study encompassed a range of taxa (five bird species, six mammals, two reptiles, one amphibian, one fish, three invertebrates, two plants), ecologies (carnivores, herbivores, omnivores, autotrophs), geographical origins (North and South America, Africa, Asia, Europe, Oceania), generation lengths (1–24 yr), and population growth rates (r = -0.07 to +0.15, as reported by the demographic analysis routine of PVA models). The 20 species are listed in Table 1, and further details on them are given in Appendix 1. The PVA input files are provided in Appendix 2; these cover the age-specific survival and reproductive rates and all stochastic effects. Table 1. Impact of inbreeding on extinction risk for 20 threatened species. The data represent median times to extinction (in years) for computer projections without inbreeding depression (MTE) and with it (MTEID) and the percentage reduction due to inbreeding depression (%) for initial populations of 50, 250, and 1000. Species Initial population size   50 250 1000     MTEID MTE %     MTEID MTE %     MTEID MTE %   Mammals     Bison bonasus  183 282 35   576 1179 51   30,112† 31,993† 6†      Gorilla gorilla     beringei  686 1293 47   55,563† 78,722† 29†   181,097 214,333 16†      Leontopithecus     rosalia  105 298 65   2146† 5033† 57†   >2000‡  >2000‡ N/A      Lipotes vexillifer  65 66 2   107 113 5   146 149 2      Loxodonta     africana  200 270 26   400 585 32   600 890 33      Panthera leo     persica  60 73 18   121 160 24   215 271 21  Birds     Amazona     vittata vittata  63 85 26   129 177 27   207 277 25      Gypaetus     barbatus  106 128 17   236 317 26   396 558 29      Nestor notabilis  164 238 31   437 668 35   929 1711 46      Tympanuchus     cupido attwateri  16 17 6   26 30 13   37 43 14      Zosterops lateralis     chlorocephala  33 56 41   93 264 65   212 825 74  Reptiles     Alligator     mississipiensis  64 70 9   142 157 10   232 301 23      Crotalus durissus     unicolor  181 297 39   749 1989 62   1,220,718† 1,822,191† 33†  Amphibians     Bufo houstonensis  34 403 92   193 >2000‡ 90   >2000‡ >2000‡ N/A  Fish     Thunnus maccoyii  23 24 4   45 46 2   64 68 6  Invertebrates     Arianta     arbustorum  30 616 95   116 >10,000 >99   384 >10,000 >96      Euphydryas     editha bayensis  17 50 66   32 117 73   53 198 73      Quadrula fragosa  88 100 12   158 189 16   239 278 14  Plants     Astragalus     cremnophylax  57 72 21   114 124 8   150 166 10      Calochortus     tiburonensis  99 295 66   260 1010 74   540 3304 84  †Mean lifespan used because MTE exceeded VORTEX's maximum duration of 2000 yr. ‡Lognormal survival analysis algorithm does not converge; median > 2000.

The individual-based generic PVA package VORTEX, version 8.4 (Miller and Lacy 1999), was used to model the age-structured populations for the 15 vertebrates and for one of the invertebrates, and the cohort-based RAMAS^® Stage, version 1.4 (Ferson 1994), was used to model the stage-structured populations of the two plants and the remaining two invertebrates. Inbreeding depression for juvenile survival is preprogrammed into VORTEX. It was instituted in RAMAS Stage using procedures devised by Burgman and Lamont (1992), except that purging was allowed for (see Appendix 3 for a full description). Because RAMAS uses a cohort-based modeling system, the cost of inbreeding represents an average across individuals. This assumption ignores some of the potential complexities involved in coupling ecological and genetic dynamics. However, RAMAS and VORTEX gave concordant results when compared on the same species with inbreeding depression included (Brook et al. 2000), which implies that our results were not sensitive to this simplification

Because there are quantitative data on inbreeding depression for only a relatively few species, we applied a conservative value of 3.14 lethal equivalents per diploid genome on juvenile mortality. This resulted in an elevated death rate for inbred individuals before they reached breeding age, which may increase the effectiveness of purging. The value of 3.14 lethal equivalents is the median value from a study of 40 captive vertebrate populations (Ralls et al. 1988). The International Union for Conservation of Nature and Natural Resources (2000) "red lists" more than 50% of mammals as threatened, including 25 of the 40 mammalian species examined by Ralls et al. (1988). There are no clear differences in inbreeding depression between major taxa for diploid species (Ralls et al. 1988, Frankham 1998, Crnokrak and Roff 1999). This estimate is conservative, because inbreeding effects occur not only for juvenile mortality but also for adult mortality, reproductive rates, mating ability, etc. (Lynch and Walsh 1998) and are greater in the wild than in captivity (Crnokrak and Roff 1999). In the two cases for which we had direct data, the American alligator (Alligator mississippiensis) and the golden lion tamarin (Leontopithecus rosalia), we used species-specific estimates of lethal equivalents: 4.07 and 5.0, respectively.

Random mating was applied, because this is an assumption inherent in most of the literature on inbreeding in finite populations (see Falconer and Mackay 1996); it is also valid in our case because we do not apply inbreeding depression to mating. Initial conditions assume that levels of inbreeding (F) = 0, although F is always defined relative to some arbitrary starting point (Falconer and Mackay 1996). Based on the only reliable data from Drosophila (Simmons and Crow 1977), half of the inbreeding depression was assumed to be caused by recessive lethal alleles and therefore subject to purging. The other half was attributed to sublethal alleles of smaller effect that are not much affected by purging. Purging is achieved in VORTEX through both selection and genetic drift (Miller and Lacy 1999). These values are widely accepted as reasonable, and no credible alternative values for these purging parameters exist in the literature.

Catastrophe regimes defined by studies on the particular species were used when available. When no information was available on catastrophes for a species, a default regime of 5% probability of catastrophes per year was applied, based on Mangel and Tier (1994), and a regime of effects was devised by consolidating the data from Fig. 1 in Young (1994) into five independent catastrophe classes. The individual catastrophes imposed an additional 32, 47, 62, 77, or 93% mortality, with a probability of occurrence for each class of 1% per annum.

Initial population sizes (N) of 50, 250, and 1000 were used, corresponding approximately to the red-listed categories of "critically endangered," "endangered," and "vulnerable," respectively (International Union for Conservation of Nature and Natural Resources 2000). Insects, small vertebrates, and short-lived plants are widely viewed as having large environmental fluctuations and larger minimum viable population sizes than do large vertebrates and long-lived plants. However, these differences largely disappeared when they were compared on a per generation basis (Sinclair 1996). Because inbreeding operates on a per generation basis (Falconer and Mackay 1996), the effects of inbreeding depression might be expected to be relatively comparable across taxa.

The rate of population growth modeled in the 20 populations mainly reflects historical ecological and human impacts. Although past inbreeding may have had a secondary effect, inbreeding results in an approximately linear decline in fitness with F (see Fig. 14.1 in Falconer and Mackay 1996), so it matters little if populations previously had an F of, say, 0.2. As indicated above, the measure of 3.14 lethal equivalents we use for inbreeding depression derives predominantly from threatened species. Furthermore, any overestimate of the impact of inbreeding depression because of the implicit inclusion of past inbreeding impacts (see Brook 2000) pales into insignificance compared to researchers' underestimates of the impact of inbreeding depression resulting from the fact that they have (1) applied inbreeding depression only to juvenile survival when actual values are up to 3.3 times greater over the full life cycle (see Frankel and Soulé 1981) and (2) taken data from captive populations and applied it to the wild, where inbreeding depression can be up to seven times greater (see Crnokrak and Roff 1999).

All natural populations of threatened species have limited habitat, and it is unrealistic to assume exponential growth. A ceiling carrying capacity (K) of twice the initial population size was therefore imposed in each case. This is a conservative way of representing habitat limitation, because functional forms of density dependence tend to strongly affect extinction risk (Ginzburg et al. 1990) and generally require the estimation of many additional parameters.

All stochastic simulations were replicated 1000 times and projected forward to estimate median times to extinction. This parameter was used because it has an unbounded scale, in contrast to proportion extinct. In addition, this measure is not biased by occasional run times that are extremely long, which is a problem with mean time to extinction. Most analyses were done using the percentage difference in median time to extinction between the models for a species with inbreeding depression (MTE_ID) and without it (MTE), computed as 100*(MTE - MTE_ID)/MTE.

It was not feasible to obtain estimates of MTE in every case, because the VORTEX package has a maximum run length of 2000 yr. In these cases, simulations were projected for 25 generations, and the survivorship curves, i.e., 1 - PE(cumulative) for 1000 populations, were fitted to the lognormal distribution as theoretically predicted by Sæther et al. (2000), with a correction for censored observations, i.e., populations surviving beyond 25 generations, using the parametric regression program in JMP, version 4.04 (SAS Institute 2000). The presence or absence of inbreeding was introduced as a categorical predictor variable, and mean lifespan (ML) was estimated as exp(μ + μ_ID + 0.5·ς²), where μ and ς are fitted parameters. This yielded unbiased estimates of the mean time to extinction (lifespan) with and without inbreeding depression. As with the median times to extinction, the percentage difference was calculated as 100*(ML - ML_ID)/ML. In a few cases, the lognormal survival analysis algorithm did not converge, so no estimate was obtained. Inclusion vs. exclusion of species lifespan estimates did not alter these conclusions.

Statistical analyses

The resulting statistics were analyzed by nonparametric methods, because percent differences were not normally distributed. Wilcoxon signed-rank tests were used to test whether the differences for each of the three population sizes and for various groups of taxa were greater than zero. Variation among major taxa was tested using Mood's median test, whereas differences among population sizes and among individual taxa were assessed using Friedman's test (see Sokal and Rohlf 1995). The significance of the relationship between percent differences and population replacement rates was tested using Spearman's rank correlation. All tests were done using MINITAB, version 12, statistical software (Ryan et al. 1994).

Projected population sizes and extinction risk

All 20 species showed a pattern of lower population sizes with inbreeding depression than without it that eventually translated into a higher extinction risk with inbreeding depression. However, the magnitude of the impact of inbreeding depression varied considerably across different species. Population trajectories for four representative species are illustrated in Fig. 1. The median times to extinction for all 20 species are summarized in Table 1. The probabilities of extinction, mean final population sizes, and % heterozygosity remaining after 100 yr, with and without inbreeding depression, are listed in Table 2.

Fig. 1. The left-hand graph of each pair shows the impact of inbreeding depression on mean persisting population size, Mean N, and the right-hand graph shows the cumulative probability of extinction, P[E], for four representative species over a period of 100 yr. These values were determined using population viability analysis with all demographic, environmental, and catastrophic effects in operation.

Table 2. Probability of extinction P(E), mean final population size (N), and percentage of heterozygosity remaining (H) after 100 yr for each species at initial population sizes of 50, 250, and 1000 individuals for simulations with and without inbreeding modeled. Species Inbreeding Initial population size     50 250 1000      P(E) N H   P(E) N H   P(E) N H  Alligator Yes  0.686 55 0.811   0.353 248 0.925   0.238 822 0.898  mississipiensis No  0.697 60 0.792   0.315 267 0.866   0.176 938 0.958  Amazona Yes  0.829 22 0.748   0.287 103 0.905   0.052 435 0.961  vittata vittata No  0.615 38 0.742   0.18 127 0.896   0.036 486 0.964  Arianta Yes  0.37 22 0.53   0 503 0.96   0 2056 1  arbustorum No  0 100 0.68   0 514 0.97   0 2062 0.96  Astragalus Yes  0.791 19 0.303   0.444 54 0.554   0.181 209 0.783  cremnophylax No  0.755 24 0.324   0.387 68 0.589   0.158 213 0.796  Bison Yes  0.246 74 0.848   0.055 369 0.954   0.014 1473 0.986  bonasus No  0.199 80 0.834   0.056 379 0.952   0.01 1579 0.984  Bufo Yes  1 0 0   0.002 418 0.776   0 1969 0.943  houstonensis No  0.16 78 0.209   0 482 0.782   0 1979 0.942  Calochortus Yes  0.47 38 0.56   0.085 263 0.896   0.044 1185 0.975  tiburonensis No  0.17 63 0.74   0.029 299 0.938   0.008 1265 0.981  Crotalus durissus Yes  0.281 66 0.762   0.053 354 0.933   0.005 1430 0.982  unicolor No  0.206 74 0.74   0.036 359 0.931   0.003 1464 0.981  Euphydryas Yes  1 0 0   0.99 18 0.17   0.85 527 0.28  editha bayensis No  0.72 86 0.22   0.47 347 0.35   0.26 1462 0.54  Gorilla gorilla Yes  0.039 77 0.947   0.002 390 0.988   0.001 1565 0.997  beringei No  0.04 80 0.941   0.006 398 0.987   0 1572 0.997  Gypaetus Yes  0.475 31 0.873   0.06 167 0.959   0 664 0.99  barbatus No  0.358 35 0.856   0.035 180 0.957   0.001 742 0.989  Leontopithecus Yes  0.475 43 0.807   0.008 353 0.959   0 1580 0.99  rosalia No  0.173 65 0.794   0.004 385 0.959   0 1591 0.99  Lipotes Yes  0.926 6 0.794   0.413 11 0.927   0.033 34 0.976  vexillifer No  0.841 8 0.762   0.338 12 0.911   0.028 38 0.97  Loxodonta Yes  0.165 45 0.925   0.022 236 0.98   0.006 915 0.994  africana No  0.151 48 0.916   0.024 236 0.976   0.003 904 0.994  Nestor Yes  0.31 69 0.863   0.097 344 0.959   0.026 1421 0.986  notabilis No  0.262 73 0.849   0.071 343 0.95   0.019 1388 0.983  Panthera leo Yes  0.747 53 0.74   0.393 232 0.894   0.187 901 0.951  persica No  0.639 62 0.705   0.332 264 0.872   0.158 937 0.938  Quadrula Yes  0.613 17 0.825   0.1 69 0.941   0.014 272 0.965  fragosa No  0.5 25 0.789   0.069 80 0.935   0.005 283 0.981  Thunnus Yes  1 0 0   1 0 0   0.988 5 0.628  maccoyii No  1 0 0   0.998 6 0.6   0.978 14 0.773  Tympanuchus Yes  1 0 0   1 0 0   0.996 81 0.72  cupido attwateri No  0.999 2 0   0.981 65 0.362   0.931 222 0.487  Zosterops lateralis Yes  0.997 12 0.457   0.552 144 0.856   0.096 867 0.951  chlorocephala No  0.763 44 0.52   0.165 261 0.846   0.025 1039 0.949

Differences in median times to extinction due to inbreeding depression

For N = 50, median times to extinction with inbreeding were shorter than those without inbreeding for all 20 species (Table 1). The mean reduction attributable to inbreeding was 36%, and the median 28.5% (Wilcoxon W = 210, P < 0.001). Results for N = 250 and 1000 yielded conclusions similar to those for N = 50 (Table 1). The mean and median percent differences attributable to inbreeding depression were 40 and 30.5%, respectively, for N = 250 (Wilcoxon W = 210, P < 0.001) and 34 and 25%, respectively, for N = 1000 (W = 171, P < 0.001).

For the same 14 species with complete MTE data, the impact of inbreeding differed slightly but significantly with population size, giving medians of 19, 24, and 26% for N = 50, 250, and 1000, respectively (Friedman S = 12.0, df = 2, P = 0.002).

Comparisons among taxa with regard to the impact of inbreeding depression

There were significant differences among species in terms of the impact of inbreeding on extinction risk (Friedman S = 36.9, df = 13, P < 0.001). However, the impact of inbreeding was similar across major taxa, which is to be expected if the effects of inbreeding depression scale to generations. There was no significant variation among mammals, birds, poikilotherm vertebrates, invertebrates, or plants in the magnitude of the difference (Mood's median test M = 0.53, df = 4, P = 0.97). Tests of the impact of inbreeding for N = 50 and N = 250 (for which the data were complete) were significant for all taxa (see above), including vertebrates (Wilcoxon W = 120, P < 0.001), mammals (W = 21, P = 0.02), birds (W = 15, P = 0.03), and invertebrates plus plants (W = 15, P = 0.03). A full exploration of any potential differences arising from different life history strategies or ecologies would require the examination of many more species. However, we do not know of any evidence to date that relates inbreeding depression to life histories.

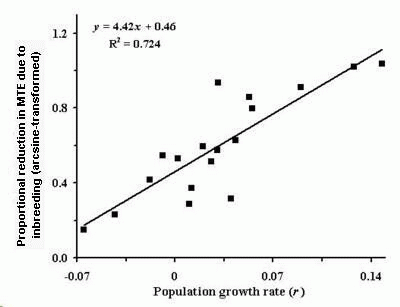
Relationship between impact of inbreeding and population growth rate

The major variable explaining differences among species with regard to the impact of inbreeding was the initial intrinsic population growth rate (r). As seen in Fig. 2, the relationship for N = 250 runs was positive and highly significant (Spearman's rank correlation = 0.831, P < 0.001). Similar relationships were evident at all population sizes.

Fig. 2. Relationship between initial population growth rate and inbreeding depression expressed as arcsine-transformed proportionate decrease in median time to extinction (MTE). The relationship is highly significant (Spearman's rank correlation = 0.831, p < 0.001).

Inbreeding depression markedly reduced the time to extinction for a broad range of threatened taxa; the median reduction in median time to extinction (MTE) was 25–31%. This was consistent across initial population sizes of 50, 250, and 1000, and there were no obvious differences among major taxa. However, there was a strong effect of initial population growth rate. These impacts of inbreeding will be underestimates (see Methods). Our findings indicate that evidence from a few species (Dobson et al. 1992, Newman and Pilson 1997, Saccheri et al. 1998, Oostermeijer 2000) applies across a wide range of taxa. Claims that purging will eliminate the impact of inbreeding depression on extinction risk are refuted by our results.

Independent evidence that populations are not driven to extinction before genetic factors can affect them comes from comparisons of levels of genetic diversity in endangered and related nonendangered species. Genetic diversity between endangered and related nonendangered species is a widely accepted comparison for general meta-analyses (see Frankham 1995a, Haig and Avise 1996, Frankham 2000) and for innumerable individual species such as the cheetah (May 1995), northern hair-nosed wombat (Taylor et al. 1994), Mariana crow, Ethiopian wolf, Mauritius kestrel, and others (see Frankham et al. 2002, Chapter 3). Most endangered species have less genetic diversity than related nonendangered species (see references above; D. Spielman, B.W. Brook, and R. Frankham, unpublished data), although there are a few examples, e.g., the Indian rhinoceros (Dinerstein and McCracken 1990), that do not fit this general pattern. Because the proportionate loss of heterozygosity equals the inbreeding coefficient (Falconer and Mackay 1996), most endangered species are already inbred. If "nongenetic" factors drove species to extinction before inbreeding was a problem, there would be no such difference. Further, loss of genetic diversity is related to reduced fitness (Reed and Frankham 2002). Although there are a number of ecological factors that may also plausibly correlate with standing crops of genetic variation, the evidence for these is weak and inconsistent. The predominant factor explaining differences in levels of genetic variation among species is population size: Soulé (1976) and Frankham (1996) attribute approximately 50 and 72% of this variation to population size, respectively. In addition, a careful examination of the ecological predictors presented in Nevo et al. (1975) reveals that these are likely to be surrogates of population size. Other explanatory factors include phylogeny (vertebrates, invertebrates, plants, etc.) and range extent, both of which can also be explained as an effect of population size (Frankham et al. 2002).

Why did other researchers conclude that inbreeding depression has little impact on extinction risk? One reason is the time factor. The study by Burgman and Lamont (1992) considered only a few generations. In contrast, our study was not affected by duration because we took populations to extinction. Lande (1988) and others have suggested that other factors would be likely to cause extinctions before inbreeding depression became a problem. Our study has shown that the impact of inbreeding is less when the population growth rate is negative, as often happens as a result of human impacts. However, this effect has been severely overestimated, given the overall picture revealed by our results.

In what circumstances is inbreeding depression likely to make important contributions to extinction risk? Our results indicate that it will be important for most naturally outbreeding diploid species. However, inbreeding will have little time to act in populations that are declining rapidly due to deterministic pressures such as habitat loss (see Fig. 2). Inbreeding will have less impact on naturally inbreeding species, because on average they have lower inbreeding depression (see Husband and Schemske 1996). It will probably be less in species with polyploid ancestry, because they seem to suffer less inbreeding depression than do equivalent diploids (Husband and Schemske 1997). Species that exhibit large variations in population size due to demographic and environmental stochasticity and catastrophes are likely to be particularly sensitive to inbreeding. Populations that have had very small effective population sizes (N_e < 500) for a long time, or those that have recovered from population bottlenecks, should be less sensitive to inbreeding depression due to the purging of deleterious recessive alleles. However, the effects of purging often seem to be relatively small (see Byers and Waller 1999, Miller and Hedrick 2001); Frankham et al. (2001) found no significant difference in extinction risk between purged populations (formed by crossing very highly inbred populations) and nonpurged, wild, outbred populations when both were deliberately inbred.

Our results have important conservation implications. First, ignoring inbreeding depression will substantially underestimate extinction risk. Many population viabilitiy analyses (PVAs) have been and still are being carried out without considering inbreeding depression. Almost all PVAs done using RAMAS software have omitted inbreeding depression, as have most PVAs done using software written for case-specific analysis. We are aware of only two plant PVAs that included inbreeding depression (Burgman and Lamont 1992, Oostermeijer 2000). Even those PVAs done using VORTEX software, which normally incorporates inbreeding depression, include it only for juvenile survival, despite the fact that inbreeding depression affects all components of the life cycle (Frankel and Soulé 1981).

The second concern is that inappropriate recovery programs may be devised if inbreeding depression is not taken into account. Reproductive fitness is normally improved if inbred populations are outcrossed (see Westemeier et al. 1998, Madsen et al. 1999, Ebert et al. 2002). If this is not done, an inbred population with low fitness may continue to decline, as happened with the Illinois population of the greater prairie chicken, Tympanuchus cupido (Westemeier et al. 1998). Attempts to recover the population by habitat improvement failed to halt its decline, and it recovered only after outcrossing with a population from another state. Third, the relative impact of inbreeding on median time to extinction (MTE) is similar over a range of different population sizes (although the absolute value of MTE increases as population size increases), and even relatively large populations (N = 1000) are susceptible to the deleterious effects of inbreeding. This is because the inbreeding coefficient increases rapidly when N_e is temporarily reduced because of fluctuations in population size and is not subsequently mitigated (a "ratchet effect"), except through migration. Further, the relative impact of all stochastic effects on extinction risk decreases with increasing population size (see Menges 1992, Frankham et al. 2002). Fourth, funding priorities for conservation and restoration will be distorted if the impacts of different factors on extinction risk are not correctly understood.

Our results provide strong evidence that inbreeding depression elevates extinction risk in most outbreeding threatened species. They emphasize the importance of avoiding inbreeding and maintaining genetic diversity in species of concern to conservationists.

Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.

We thank K. B. Kulasekera for his valuable advice on the statistical analyses, and Sam Scheiner and two anonymous referees for their comments on the manuscript. This study was supported by grants from Macquarie University, where the first two authors carried out much of the work for this paper, and the Australian Research Council.

Table A.1. Details of the species modeled in this study, including the major references used to provide the data for developing and assigning parameters to the population viability analysis models.

Species	Common name	Population	Threat	Generation	Major reference
		growth rate	status	length
Alligator mississipiensis	American alligator	0.04	T†	21	Kushlan and Jacobsen (1990)
Amazona vittata vittata	Puerto Rican parrot	-0.01	CR	8	Lacy et al. (1989)
Arianta arbustorum	Swiss land snail	0.001	T	4	Akçakaya and Baur (1996)
Astragalus cremnophylax	Sentry milk-vetch	0.01	CR	9	Maschinski et al. (1997)
Bison bonasus	European bison	0.058	EN	10	Pucek et al. (1996)
Bufo houstonensis	Houston toad	0.097	EN	2	Seal (1994b)
Calochortus tiburonensis	Mariposa lily	0.148	T†	11	Fiedler (1987)
Crotalus durissus unicolor	Aruba Is. rattlesnake	0.09	CR	9	CBSG (1992)
Euphydryas editha bayensis	Bay checkerspot butterfly	0.128	T†	1	Murphy et al. (1990)
Gorilla gorilla beringei	Mountain gorilla	0.038	CR	23	Werikhe et al. (1997)
Gypaetus barbatus	Bearded Vulture	0.002	T	14	Bustamante (1996)
Leontopithecus rosalia	Golden lion tamarin	0.053	CR	8	Ballou et al. (1997)
Lipotes vexillifer	Baiji dolphin	-0.04	CR	17	Kaiya et al. (1994)
Loxodonta africana	African elephant	0.02	EN	24	Armbruster and Lande (1993)
Nestor notabilis	Kea	0.043	VU	12	Seal et al. (1991)
Panthera leo persica	Asiatic lion	0.04	CR	8	Ashraf et al. (1995)
Quadrula fragosa	Mapleleaf mussel	-0.02	CR	16	Kjos et al. (1998)
Thunnus maccoyii	Southern bluefin tuna	-0.07	CR	11	Matsuda et al. (1998)
Tympanuchus cupido attwateri	Attwater's Prairie Chicken	0.012	T‡	3	Seal (1994a)
Zosterops lateralis chlorocephala	Heron Island silvereye	0.031	VU	3	Brook and Kikkawa (1998)

Note: Each species is assigned a category from the IUCN Red List of Threated Species from the International Union for Conservation of Nature and Natural Resources. In decreasing order of threat, these are: critically endangered (CR), endangered (EN), vulnerable (VU), and lower risk (LR). T denotes species that are not categorized under the IUCN Red List system but are considered to be a nationally threatened species. The national threat status assigned by the responsible agency is given where known.
^†Listed as "threatened" by the U.S. government.
^‡Listed as "endangered"

AA.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
530     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
5.000000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
N     ***EV concordance between repro and surv?***
5     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
11     ***Female Breeding Age***
14     ***Male Breeding Age***
50     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
0     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
46.60  **breeding
13.70  **EV-breeding
19.000000   ***Pop1: Mean Litter Size***
4.500000   ***Pop1: SD in Litter Size***
62.800000  *FMort age 0
7.000000  ***EV
41.100000  *FMort age 1
13.000000  ***EV
25.000000  *FMort age 2
10.000000  ***EV
25.000000  *FMort age 3
10.000000  ***EV
25.000000  *FMort age 4
10.000000  ***EV
25.000000  *FMort age 5
10.000000  ***EV
20.000000  *FMort age 6
10.000000  ***EV
3.000000  *FMort age 7
1.000000  ***EV
3.000000  *FMort age 8
1.000000  ***EV
3.000000  *FMort age 9
1.000000  ***EV
3.000000  *FMort age 10
1.000000  ***EV
3.000000  *Adult FMort
1.000000  ***EV
62.800000  *MMort age 0
7.000000  ***EV
41.100000  *MMort age 1
13.000000  ***EV
25.000000  *MMort age 2
10.000000  ***EV
25.000000  *MMort age 3
10.000000  ***EV
25.000000  *MMort age 4
10.000000  ***EV
25.000000  *MMort age 5
10.000000  ***EV
20.000000  *MMort age 6
10.000000  ***EV
3.000000  *MMort age 7
1.000000  ***EV
3.000000  *MMort age 8
1.000000  ***EV
3.000000  *MMort age 9
1.000000  ***EV
3.000000  *MMort age 10
1.000000  ***EV
3.000000  *MMort age 11
1.000000  ***EV
3.000000  *MMort age 12
1.000000  ***EV
3.000000  *MMort age 13
1.000000  ***EV
3.000000  *Adult MMort
1.000000  ***EV
1.000000     ***Probability Of Catastrophe 1***
1.000000  ***Severity--Reproduction***
0.680000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 2***
1.000000  ***Severity--Reproduction***
0.530000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 3***
1.000000  ***Severity--Reproduction***
0.380000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 4***
1.000000  ***Severity--Reproduction***
0.230000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 5***
1.000000  ***Severity--Reproduction***
0.070000  ***Severity--Survival***
N     ***All Males Breeders?***
Y     ***Answer--A--Known?***
23.750000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

AE.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000  ***Simulations***
115     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
3     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
2     ***Female Breeding Age***
2     ***Male Breeding Age***
12     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
2     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
100.00  **breeding
0.00  **EV-breeding
57.000000  ***Pop1: Percent Litter Size 1***
50.000000  *FMort age 0
0.000000  ***EV
11.300000  *FMort age 1
0.000000  ***EV
17.100000  *Adult FMort
0.000000  ***EV
50.000000  *MMort age 0
0.000000  ***EV
11.300000  *MMort age 1
0.000000  ***EV
21.400000  *Adult MMort
0.000000  ***EV
41.000000     ***Probability Of Catastrophe 1***
1.000000     ***Severity--Reproduction***
0.973000     ***Severity--Survival***
10.000000     ***Probability Of Catastrophe 2***
1.000000     ***Severity--Reproduction***
0.458000     ***Severity--Survival***
2.000000     ***Probability Of Catastrophe 3***
1.000000     ***Severity--Reproduction***
0.272000     ***Severity--Survival***
N     ***All Males Breeders?***
Y     ***Answer--A--Known?***
50.000000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

AIR.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000  ***Simulations***
235     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
N     ***EV concordance between repro and surv?***
2     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
5     ***Female Breeding Age***
5     ***Male Breeding Age***
20     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
12     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
pop1
58.00  **breeding
10.00  **EV-breeding
0.000000     ***pop1: Percent Litter Size 1***
0.000000     ***pop1: Percent Litter Size 2***
0.000000     ***pop1: Percent Litter Size 3***
0.000000     ***pop1: Percent Litter Size 4***
0.000000     ***pop1: Percent Litter Size 5***
0.000000     ***pop1: Percent Litter Size 6***
0.000000     ***pop1: Percent Litter Size 7***
10.000000     ***pop1: Percent Litter Size 8***
25.000000     ***pop1: Percent Litter Size 9***
30.000000     ***pop1: Percent Litter Size 10***
25.000000     ***pop1: Percent Litter Size 11***
70.000000  *FMort age 0
10.200000  ***EV
30.000000  *FMort age 1
10.200000  ***EV
20.000000  *FMort age 2
10.200000  ***EV
10.000000  *FMort age 3
10.200000  ***EV
10.000000  *FMort age 4
10.200000  ***EV
10.000000  *Adult FMort
10.200000  ***EV
70.000000  *MMort age 0
10.200000  ***EV
30.000000  *MMort age 1
10.200000  ***EV
20.000000  *MMort age 2
10.200000  ***EV
10.000000  *MMort age 3
10.200000  ***EV
10.000000  *MMort age 4
10.200000  ***EV
10.000000  *Adult MMort
10.200000  ***EV
14.285710     ***Probability Of Catastrophe 1***
0.000000     ***Severity--Reproduction***
1.000000     ***Severity--Survival***
2.000000     ***Probability Of Catastrophe 2***
0.250000     ***Severity--Reproduction***
0.250000     ***Severity--Survival***
N     ***All Males Breeders?***
Y     ***Answer--A--Known?***
50.000000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

AL.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
196     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
5     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
4     ***Female Breeding Age***
5     ***Male Breeding Age***
15     ***Maximum Breeding Age***
38.000000     ***Sex Ratio (percent males)***
5     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
pop1
40.00  **breeding
12.50  **EV-breeding
20.000000     ***pop1: Percent Litter Size 1***
37.500000     ***pop1: Percent Litter Size 2***
25.000000     ***pop1: Percent Litter Size 3***
15.000000     ***pop1: Percent Litter Size 4***
50.000000  *FMort age 0
33.300000  ***EV
10.000000  *FMort age 1
3.000000  ***EV
10.000000  *FMort age 2
3.000000  ***EV
10.000000  *FMort age 3
3.000000  ***EV
10.000000  *Adult FMort
3.000000  ***EV
50.000000  *MMort age 0
33.300000  ***EV
10.000000  *MMort age 1
3.000000  ***EV
10.000000  *MMort age 2
3.000000  ***EV
10.000000  *MMort age 3
3.000000  ***EV
10.000000  *MMort age 4
3.000000  ***EV
10.000000  *Adult MMort
3.000000  ***EV
1.000000     ***Probability Of Catastrophe 1***
1.000000  ***Severity--Reproduction***
0.680000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 2***
1.000000  ***Severity--Reproduction***
0.530000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 3***
1.000000  ***Severity--Reproduction***
0.380000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 4***
1.000000  ***Severity--Reproduction***
0.230000  ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 5***
1.000000  ***Severity--Reproduction***
0.070000  ***Severity--Survival***
N     ***All Males Breeders?***
Y     ***Answer--A--Known?***
50.000000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

APC.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
100     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
2     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
1     ***Female Breeding Age***
2     ***Male Breeding Age***
9     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
14     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
100.00  **breeding
12.50  **EV-breeding
0.000000     ***Pop1: Percent Litter Size 1***
0.000000     ***Pop1: Percent Litter Size 2***
0.000000     ***Pop1: Percent Litter Size 3***
0.000000     ***Pop1: Percent Litter Size 4***
0.000000     ***Pop1: Percent Litter Size 5***
0.000000     ***Pop1: Percent Litter Size 6***
0.000000     ***Pop1: Percent Litter Size 7***
0.000000     ***Pop1: Percent Litter Size 8***
0.000000     ***Pop1: Percent Litter Size 9***
0.100000     ***Pop1: Percent Litter Size 10***
2.400000     ***Pop1: Percent Litter Size 11***
95.000000     ***Pop1: Percent Litter Size 12***
2.400000     ***Pop1: Percent Litter Size 13***
91.400000  *FMort age 0
7.200000  ***EV
40.000000  *Adult FMort
5.000000  ***EV
91.400000  *MMort age 0
7.200000  ***EV
40.000000  *MMort age 1
5.000000  ***EV
40.000000  *Adult MMort
5.000000  ***EV
1.430000     ***Probability Of Catastrophe 1***
1.000000  ***Severity--Reproduction***
0.250000  ***Severity--Survival***
17.400000     ***Probability Of Catastrophe 2***
0.000000  ***Severity--Reproduction***
1.000000  ***Severity--Survival***
N     ***All Males Breeders?***
Y     ***Answer--A--Known?***
10.000000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

BD.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
428     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
0     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
8     ***Female Breeding Age***
6     ***Male Breeding Age***
30     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
1     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
pop1
40.00  **breeding
20.00  **EV-breeding
52.700000  *FMort age 0
18.800000  ***EV
20.900000  *FMort age 1
6.270000  ***EV
10.500000  *FMort age 2
3.150000  ***EV
10.500000  *FMort age 3
3.150000  ***EV
10.500000  *FMort age 4
3.150000  ***EV
10.500000  *FMort age 5
3.150000  ***EV
10.500000  *FMort age 6
3.150000  ***EV
10.500000  *FMort age 7
3.150000  ***EV
6.200000  *Adult FMort
1.900000  ***EV
52.700000  *MMort age 0
18.800000  ***EV
20.900000  *MMort age 1
6.270000  ***EV
10.500000  *MMort age 2
3.150000  ***EV
10.500000  *MMort age 3
3.150000  ***EV
10.500000  *MMort age 4
3.150000  ***EV
10.500000  *MMort age 5
3.150000  ***EV
6.200000  *Adult MMort
1.900000  ***EV
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

BV.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
355     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
1     ***Types Of Catastrophes***
M     ***Monogamous, Polygynous, or Hermaphroditic***
7     ***Female Breeding Age***
7     ***Male Breeding Age***
31     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
1     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
51.00  **breeding
16.88  **EV-breeding
21.800000  *FMort age 0
8.300000  ***EV
9.40000  *FMort age 1
9.100000  ***EV
9.40000  *FMort age 2
9.100000  ***EV
9.40000  *FMort age 3
9.100000  ***EV
9.40000  *FMort age 4
9.100000  ***EV
9.40000  *FMort age 5
9.100000  ***EV
9.40000  *FMort age 6
9.100000  ***EV
9.40000  *Adult FMort
9.100000  ***EV
21.800000  *MMort age 0
8.300000  ***EV
9.40000  *MMort age 1
9.100000  ***EV
9.40000  *MMort age 2
9.100000  ***EV
9.40000  *MMort age 3
9.100000  ***EV
9.40000  *MMort age 4
9.100000  ***EV
9.40000  *MMort age 5
9.100000  ***EV
9.40000  *MMort age 6
9.100000  ***EV
9.40000  *Adult MMort
9.100000  ***EV
1.000000     ***Probability Of Catastrophe 1***
0.500000     ***Severity--Reproduction***
0.750000     ***Severity--Survival***
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

EB.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
245     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
1     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
4     ***Female Breeding Age***
5     ***Male Breeding Age***
22     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
1     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
47.20  **breeding
9.70  **EV-breeding
10.320000  *FMort age 0
5.980000  ***EV
3.530000  *FMort age 1
3.000000  ***EV
6.550000  *FMort age 2
5.532170  ***EV
3.870000  *FMort age 3
2.680000  ***EV
7.480000  *Adult FMort
3.400000  ***EV
9.400000  *MMort age 0
6.695010  ***EV
7.040000  *MMort age 1
6.837070  ***EV
3.290000  *MMort age 2
3.719370  ***EV
3.660000  *MMort age 3
5.420670  ***EV
5.850000  *MMort age 4
5.867160  ***EV
10.380000  *Adult MMort
4.060000  ***EV
1.000000     ***Probability Of Catastrophe 1***
1.000000     ***Severity--Reproduction***
0.100000     ***Severity--Survival***
N     ***All Males Breeders?***
Y     ***Answer--A--Known?***
78.000000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

GLT.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000  ***Simulations***
193     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
4.070000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
N     ***EV concordance between repro and surv?***
4     ***Types Of Catastrophes***
M     ***Monogamous, Polygynous, or Hermaphroditic***
4     ***Female Breeding Age***
4     ***Male Breeding Age***
16     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
5     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
75.70  **breeding
38.20  **EV-breeding
20.770000     ***Pop1: Percent Litter Size 1***
57.940000     ***Pop1: Percent Litter Size 2***
5.420000     ***Pop1: Percent Litter Size 3***
15.210000     ***Pop1: Percent Litter Size 4***
32.800000  *FMort age 0
8.700000  ***EV
19.600000  *FMort age 1
13.300000  ***EV
24.600000  *FMort age 2
7.600000  ***EV
21.000000  *FMort age 3
0.000000  ***EV
12.500000  *Adult FMort
6.700000  ***EV
29.800000  *MMort age 0
7.000000  ***EV
19.700000  *MMort age 1
9.900000  ***EV
23.900000  *MMort age 2
0.000000  ***EV
17.200000  *MMort age 3
7.500000  ***EV
16.000000  *Adult MMort
8.200000  ***EV
7.000000     ***Probability Of Catastrophe 1***
1.000000     ***Severity--Reproduction***
0.900000     ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 2***
1.000000     ***Severity--Reproduction***
0.500000     ***Severity--Survival***
33.333333     ***Probability Of Catastrophe 3***
1.000000     ***Severity--Reproduction***
0.990000     ***Severity--Survival***
5.000000     ***Probability Of Catastrophe 4***
1.000000     ***Severity--Reproduction***
0.950000     ***Severity--Survival***
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

HIS.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
100     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
2     ***Types Of Catastrophes***
M     ***Monogamous, Polygynous, or Hermaphroditic***
1     ***Female Breeding Age***
1     ***Male Breeding Age***
11     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
0     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
77.50  **breeding
8.20  **EV-breeding
1.777800     ***Pop1: Mean Litter Size***
0.942600     ***Pop1: SD in Litter Size***
40.100000  *FMort age 0
9.354000  ***EV
35.200000  *Adult FMort
11.081630  ***EV
40.100000  *MMort age 0
9.354000  ***EV
35.200000  *Adult MMort
11.081630  ***EV
7.500000     ***Probability Of Catastrophe 1***
0.780000     ***Severity--Reproduction***
1.000000     ***Severity--Survival***
7.500000     ***Probability Of Catastrophe 2***
1.000000     ***Severity--Reproduction***
0.740000     ***Severity--Survival***
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

HT.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000  ***Simulations***
100     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
N     ***EV concordance between repro and surv?***
2     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
2     ***Female Breeding Age***
1     ***Male Breeding Age***
4     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
10     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
100.00  **breeding
0.00  **EV-breeding
0.000000     ***Pop1: Percent Litter Size 1***
0.000000     ***Pop1: Percent Litter Size 2***
0.000000     ***Pop1: Percent Litter Size 3***
0.000000     ***Pop1: Percent Litter Size 4***
0.000000     ***Pop1: Percent Litter Size 5***
0.000000     ***Pop1: Percent Litter Size 6***
0.000000     ***Pop1: Percent Litter Size 7***
0.000000     ***Pop1: Percent Litter Size 8***
0.000000     ***Pop1: Percent Litter Size 9***
0.000000  *FMort age 0
0.000000  ***EV
80.000000  *FMort age 1
1.000000  ***EV
80.000000  *Adult FMort
1.000000  ***EV
0.000000  *MMort age 0
0.000000  ***EV
80.000000  *Adult MMort
1.000000  ***EV
10.000000     ***Probability Of Catastrophe 1***
1.00000     ***Severity--Reproduction***
0.900000     ***Severity--Survival***
10.000000     ***Probability Of Catastrophe 2***
1.000000     ***Severity--Reproduction***
0.900000     ***Severity--Survival***
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

K.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
298     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
N     ***EV concordance between repro and surv?***
2     ***Types Of Catastrophes***
M     ***Monogamous, Polygynous, or Hermaphroditic***
5     ***Female Breeding Age***
5     ***Male Breeding Age***
25     ***Maximum Age***
50.00000     ***Sex Ratio***
4     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
pop1
40.00  **breeding
5.000000     ***EV--Reproduction***
37.500000     ***Population 1: Percent Litter Size 1***
50.000000     ***Population 1: Percent Litter Size 2***
12.500000     ***Population 1: Percent Litter Size 3***
40.000000  *FMort age 0
10.000000     ***EV--FemaleMortality***
10.000000  *FMort age 1
3.000000     ***EV--FemaleMortality***
5.000000  *FMort age 2
2.000000     ***EV--FemaleMortality***
5.000000  *FMort age 3
2.000000     ***EV--FemaleMortality***
5.000000  *FMort age 4
2.000000     ***EV--FemaleMortality***
5.000000  *Adult FMort
2.000000     ***EV--AdultFemaleMortality***
40.000000  *MMort age 0
10.000000     ***EV--MaleMortality***
10.000000  *MMort age 1
3.000000     ***EV--MaleMortality***
5.000000  *MMort age 2
2.000000     ***EV--MaleMortality***
5.000000  *MMort age 3
2.000000     ***EV--MaleMortality***
5.000000  *MMort age 4
2.000000     ***EV--MaleMortality***
5.000000  *Adult MMort
2.000000     ***EV--AdultMaleMortality***
4.000000     ***Probability Of Catastrophe 1***
0.250000     ***Severity--Reproduction***
0.800000     ***Severity--Survival***
1.000000     ***Probability Of Catastrophe 2***
0.950000     ***Severity--Reproduction***
0.100000     ***Severity--Survival***
N     ***All Males Breeders?***
90.000000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

MG.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
563     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
1     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
10     ***Female Breeding Age***
13     ***Male Breeding Age***
40     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
1     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
pop1
31.30  **breeding
5.00  **EV-breeding
23.300000  *FMort age 0
5.800000  ***EV
11.700000  *FMort age 1
2.930000  ***EV
0.000000  *FMort age 2
0.500000  ***EV
7.400000  *FMort age 3
1.900000  ***EV
2.900000  *FMort age 4
0.700000  ***EV
0.000000  *FMort age 5
0.500000  ***EV
0.000000  *FMort age 6
0.500000  ***EV
3.800000  *FMort age 7
0.950000  ***EV
4.400000  *FMort age 8
1.100000  ***EV
0.000000  *FMort age 9
0.500000  ***EV
1.000000  *Adult FMort
0.250000  ***EV
20.000000  *MMort age 0
5.000000  ***EV
1.600000  *MMort age 1
0.400000  ***EV
5.500000  *MMort age 2
1.400000  ***EV
6.400000  *MMort age 3
1.600000  ***EV
2.500000  *MMort age 4
0.700000  ***EV
0.000000  *MMort age 5
0.500000  ***EV
0.000000  *MMort age 6
0.500000  ***EV
0.000000  *MMort age 7
0.500000  ***EV
0.000000  *MMort age 8
0.500000  ***EV
0.000000  *MMort age 9
0.500000  ***EV
0.000000  *MMort age 10
0.500000  ***EV
0.000000  *MMort age 11
0.500000  ***EV
0.000000  *MMort age 12
0.500000  ***EV
2.500000  *Adult MMort
0.500000  ***EV
1.000000     ***Probability Of Catastrophe 1***
1.000000  ***Severity--Reproduction***
0.250000  ***Severity--Survival***
N     ***All Males Breeders?***
Y     ***Answer--A--Known?***
70.000000     ***Percent Males In Breeding Pool***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***

MM.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
375     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
1     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
7     ***Female Breeding Age***
7     ***Male Breeding Age***
25     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
0     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
19.40  **breeding
10.00  **EV-breeding
10.000000     ***Pop1: Mean Litter Size***
10.000000     ***Pop1: SD in Litter Size***
90.000000  *FMort age 0
3.000000  ***EV
10.000000  *FMort age 1
3.000000  ***EV
10.000000  *FMort age 2
3.000000  ***EV
5.000000  *FMort age 3
2.000000  ***EV
5.000000  *FMort age 4
2.000000  ***EV
5.000000  *FMort age 5
2.000000  ***EV
5.000000  *FMort age 6
2.000000  ***EV
2.600000  *Adult FMort
0.500000  ***EV
90.000000  *MMort age 0
3.000000  ***EV
10.000000  *MMort age 1
3.000000  ***EV
10.000000  *MMort age 2
3.000000  ***EV
5.000000  *MMort age 3
2.000000  ***EV
5.000000  *MMort age 4
2.000000  ***EV
5.000000  *MMort age 5
2.000000  ***EV
5.000000  *MMort age 6
2.000000  ***EV
1.600000  *Adult MMort
0.300000  ***EV
5.000000     ***Probability Of Catastrophe 1***
0.700000     ***Severity--Reproduction***
0.700000     ***Severity--Survival***
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

PRP.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000   ***Simulations***
208     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
1     ***Types Of Catastrophes***
M     ***Monogamous, Polygynous, or Hermaphroditic***
4     ***Female Breeding Age***
4     ***Male Breeding Age***
15     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
5     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
30.70  **breeding
0.00  **EV-breeding
29.600000     ***Pop1: Percent Litter Size 1***
26.000000     ***Pop1: Percent Litter Size 2***
37.100000     ***Pop1: Percent Litter Size 3***
3.700000     ***Pop1: Percent Litter Size 4***
32.500000  *FMort age 0
3.300000  ***EV
15.200000  *FMort age 1
1.500000  ***EV
15.200000  *FMort age 2
1.500000  ***EV
15.200000  *FMort age 3
1.500000  ***EV
8.700000  *Adult FMort
0.900000  ***EV
32.500000  *MMort age 0
3.300000  ***EV
15.200000  *MMort age 1
1.500000  ***EV
15.200000  *MMort age 2
1.500000  ***EV
15.200000  *MMort age 3
1.500000  ***EV
8.700000  *Adult MMort
0.900000  ***EV
3.000000     ***Probability Of Catastrophe 1***
0.000000     ***Severity--Reproduction***
0.500000     ***Severity--Survival***
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

SBT.OUT     ***Output Filename***
Y     ***Graphing Files?***
Y     ***Details each Iteration?***
1000     ***Simulations***
273     ***Years***
1     ***Reporting Interval***
0     ***Definition of Extinction***
1     ***Populations***
Y     ***Inbreeding Depression?***
3.140000     ***Lethal equivalents***
50.000000     ***Percent of genetic load as lethals***
Y     ***EV concordance between repro and surv?***
0     ***Types Of Catastrophes***
P     ***Monogamous, Polygynous, or Hermaphroditic***
8     ***Female Breeding Age***
8     ***Male Breeding Age***
40     ***Maximum Breeding Age***
50.000000     ***Sex Ratio (percent males)***
0     ***Maximum Litter Size (0 = normal distribution) *****
N     ***Density Dependent Breeding?***
Pop1
100.00  **breeding
0.00  **EV-breeding
3.745000     ***Pop1: Mean Litter Size***
1.140000     ***Pop1: SD in Litter Size***
27.900000  *FMort age 0
5.900000  ***EV
27.900000  *FMort age 1
5.900000  ***EV
27.900000  *FMort age 2
5.900000  ***EV
27.900000  *FMort age 3
5.900000  ***EV
27.900000  *FMort age 4
5.900000  ***EV
27.900000  *FMort age 5
5.900000  ***EV
27.900000  *FMort age 6
5.900000  ***EV
27.900000  *FMort age 7
5.900000  ***EV
27.900000  *Adult FMort
5.900000  ***EV
27.900000  *MMort age 0
5.900000  ***EV
27.900000  *MMort age 1
5.900000  ***EV
27.900000  *MMort age 2
5.900000  ***EV
27.900000  *MMort age 3
5.900000  ***EV
27.900000  *MMort age 4
5.900000  ***EV
27.900000  *MMort age 5
5.900000  ***EV
27.900000  *MMort age 6
5.900000  ***EV
27.900000  *MMort age 7
5.900000  ***EV
27.900000  *Adult MMort
5.900000  ***EV
Y     ***All Males Breeders?***
Y     ***Start At Stable Age Distribution?***
250     ***Initial Population Size***
500     ***K***
0.000000     ***EV--K***
N     ***Trend In K?***
N      ***Harvest?***
N     ***Supplement?***
N     ***AnotherSimulation?***

RAMAS/stage input file (1.4) 112
Bay Checkerspot Butterfly
Dick's examples                                               
                                                                 
1000
100
-Drivers-
1
Rnorm
2
0
1

-Parameters-
6
N
1/ins((2*[st1]),1,10000000)
F
({N}+(1-{N})*tle(tim,1,0.0,{F}))/(1+{con}*{N}))
Con
0.25
Rinbr
exp([r])*exp(-1*({F}*1.57))
K
[st1]/500
r
0.128 + (0.898 * [Rnorm])
-Stages-
1
st1
250
({st1}*[Rinbr])/max(1,[K])
-Tallies-
2
Total
1
{st1}


Hcheck
1
1-[F]


-Views-
1
1
1
0

0
0
100
1
0
0.99
0
-End of file-


RAMAS/stage input file (1.4) 20
Mariposa Lily, C. tiburonensis

1000
500
-Drivers-
8
p11
2
0.74
0.55

p12
2
0.05
0.003

p13
2
1.11
1.23

p21
3
0.24
0.014

p22
3
0.87
0.19

p23
3
0.04
0.001

p32
3
0.08
0.001

p33
3
0.95
0.23

-Parameters-
8
N
(1/ins((2*[St2]+[St3]),1,10000000))/11
F
([N]+(1-[N])*tle(tim,1,0,[F]))/(1+[Con]*[N])
Sinbr
[p21]*exp(-1*([F]*1.57))
Finbr
{p11}*exp(-1*([F]*1.57))
Con
0.25
cat
if1(uni(0,1)+1/50,0.25,1.0)
KM
500
K
({St2}+{St3})/[KM]
-Stages-
3
St1
206
poi(pos([Finbr])ù{St1})+poi(pos([p12])ù{St2})+poi(pos([p13])ù{St3})
St2
181
(bin(pro([sinbr]),{St1}*[cat])+bin(pro([p22]),{St2}*[cat])+bin(pro([p23]),{St3}*[cat]))/max(1,[K])
St3
69
(bin(pro([p32]),{St2}*[cat])+bin(pro([p33]),{St3}*[cat]))/max(1,[K])
-Tallies-
2
Total
1
[St2]+[St3]


Hcheck
1
1-[F]


-Views-
1
1
1
0


0
9

0
0.99
0
-End of file-


RAMAS/stage input file (1.4) 73
Land Snail                                                

1000
1000
-Drivers-
2
Rnorm
3
0
1

Cat
1
0
1

-Parameters-
14
K
({st2}+{st3}+{st4})/[KM]
N
(1/ins((2*[st2]+[st3]+[st4]),1,10000000))/4.5
F
([N]+(1-[N])*tle(tim,1,0,[F]))/(1+[Con]*[N])
Sinbr
[s1]*exp(-1*([F]*1.57))
Con
0.25
KM
500
CatS
if1( ([Cat]+0.18), 1, 1)
fec2
0.342 + (0.171 * [Rnorm])
fec3
4.446 + (2.223 * [Rnorm])
fec4
6.84 + (3.42 * [Rnorm])
s1
0.076 + (0.0 * [Rnorm])
s2
0.8 + (0.12 + [Rnorm])
s3
0.75 + (0.11 * [Rnorm])
s4
0.56 + (0.08 * [Rnorm])
-Stages-
4
st1
1035
(poi(pos({fec2}*{st2}))+poi(pos({fec3}*{st3}))+poi(pos({fec4}*{st4})))/max(1,{k})
st2
80
(bin(pro(({cats}*{sinbr})),{st1}))/max(1,{k})
st3
65
(bin(pro(({cats}*{s2})),{st2}))/max(1,{k})
st4
105
(bin(pro({cats}*{s3}),{st3})+bin(pro({cats}*{s4}),{st4}))/max(1,{k})
-Tallies-
2
Total
10
[st2]+[st3]+[st4]


Hcheck
10
1-[F]


-Views-
1
0
1
0

0
0
1000.4
1
-0.429
581.231
0
-End of file-


RAMAS/stage input file (1.4) 13
Sentry Milk Vetch

1000
200
-Drivers-
17
f13
2
0.05
0.001

f14
2
0.48
0.094

f15
2
1.52
0.946

p21
3
0.461
0.025

p22
3
0.521
0.064

p31
3
0.259
0.007

p32
3
0.24
0.051

p33
3
0.748
0.005

p34
3
0.123
0.015

p35
3
0.02
0.01

p41
3
0.025
0.01

p42
3
0.025
0.01

p43
3
0.100
0.009

p44
3
0.783
0.031

p45
3
0.096
0.011

p54
3
0.042
0.004

p55
3
0.616
0.129

-Parameters-
7
N
(1/ins((2*[SR]+[MR]+[LR]),1,10000000))/9
F
([N]+(1-[N])*tle(tim,1,0,[F]))/(1+[Con]*[N])
Sinbr
[p21]*exp(-1*([F]*1.57))
Con
0.25
KM
500
K
({S}+{NR}+{SR}+{MR}+{LR})/{KM}
cat
if1(uni(0,1)+1/50,0.25,1.0)
-Stages-
5
S
42
(poi(pos([f13])ù{SR})+poi(pos([f14])ù{MR})+poi(pos([f15])ù{LR}))/max(1,[K])
NR
39
(bin(pro([sinbr]*[cat]),{S})+bin(pro([p22]*[cat]),{NR}))/max(1,[K])
SR
105
(bin(pro([p31]*[cat]),{S})+bin(pro([p32]*[cat]),{NR})+bin(pro([p33]*[cat]),{SR})+bin(pro([p34]*[cat]),{MR})+bin(pro([p35]*[cat]),{LR}))/max(1,[K])
MR
58
(bin(pro([p41]*[cat]),{S})+bin(pro([p42]*[cat]),{NR})+bin(pro([p43]*[cat]),{SR})+bin(pro([p44]*[cat]),{MR})+bin(pro([p45]*[cat]),{LR}))/max(1,[K])
LR
6
(bin(pro([p54]*[cat]),{MR})+bin(pro([p55]*[cat]),{LR}))/max(1,[K])
-Tallies-
2
Total
1
[S]+[NR]+[SR]+[MR]+[LR]


Hcheck
1
1-[F]


-Views-
0
-End of file-

This is the procedure we used to model inbreeding depression in RAMAS Stage. Our aim was to mimic the methods used by VORTEX, version 8 (see Miller and Lacy 1999), to model inbreeding depression, because this software program has been thoroughly scrutinized and is well established in conservation biology. Accordingly, the relationship between inbreeding and juvenile survival was modeled using an exponential decline S = S₀e^-bF, where S₀ is the survival of noninbred individuals, b is the average number of lethal equivalents per haploid genome, and F is the inbreeding coefficient (Morton et al. 1956). Following the protocols of Burgman and Lamont (1992), F was calculated automatically by the simulation model from the relationship

where 1/(2N_e) reflects new inbreeding (see Falconer and Mackay 1996), and N_e is the effective population size. N_e was calculated automatically by the model from the relationship

where N_m is the number of breeding males and N_f the number of breeding females (see Falconer and Mackay 1996).

To encompass the effects of purging, Eq. A.2 was divided by

where the correction factor k = 0.25 was derived by iteratively comparing the output of a RAMAS Stage model with the output of a VORTEX model for the same taxon and adjusting the correction factor until parity of output from the two models was obtained.

Akçakaya, H. R., and B. Baur. 1996. Effects of population subdivision and catastrophes on the persistence of a land snail metapopulation. Oecologia 105:475-483.

Akçakaya, H. R., and P. Sjögren-Gulve. 2000. Population viability analyses in conservation planning: an overview. Ecological Bulletins 48:9-21.

Armbruster, P., and R. Lande. 1993. A population viability analysis for African elephant (Loxodonta-Africana)—how big should reserves be? Conservation Biology 7:602-610.

Ashraf, N. V. K., R. Chellam, S. Molur, D. Sharma, and S. Walker. 1995. Population and habitat viability assessment P.H.V.A. workshops for Asiatic lion, Panthera leo persica, report July 1995. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Ballou, J. D. 1997. Effects of ancestral inbreeding on genetic load in mammalian populations. Journal of Heredity 88:169-178.

Beissinger, S. R., and D. R. McCullough, editors. 2002. Population viability analysis. University of Chicago Press, Chicago, Illinois, USA.

Brook, B. W. 2000. Pessimistic and optimistic bias in population viability analysis. Conservation Biology 14:564-566.

Brook, B. W., and J. Kikkawa. 1998. Examining threats faced by island birds: a population viability analysis on the Capricorn silvereye using longterm data. Journal of Applied Ecology 35:491-503.

Brook, B. W., J. J. O'Grady, A. P. Chapman, M. A. Burgman, H. R. Akçakaya, and R. Frankham. 2000. Predictive accuracy of population viability analysis in conservation biology. Nature 404:385-387.

Burgman, M. A., and B. B. Lamont. 1992. A stochastic model for the viability of Banksia cuneata populations: environmental, demographic and genetic effects. Journal of Applied Ecology 29:719-727.

Bustamante, J. 1996. Population viability analysis of captive and released Bearded Vulture populations. Conservation Biology 10:822-831.

Byers, D. L., and D. M. Waller. 1999. Do plant populations purge their genetic load? Effects of population size and mating history on inbreeding depression. Annual Review of Ecology and Systematics 30:479-513.

Caro, T. M., and M. K. Laurenson. 1994. Ecological and genetic factors in conservation: a cautionary tale. Science 263:485-486.

Caughley, G. 1994. Directions in conservation biology. Journal of Animal Ecology 63:215-244.

Conservation Breeding Specialist Group. 1992. Aruba Island rattlesnake (Crotalus durissus unicolor) population and habitat viability assessment. Conservation Breeding Specialist Group. Apple Valley, Minnesota, USA.

Crnokrak, P., and D. A. Roff. 1999. Inbreeding depression in the wild. Heredity 83:260-270.

Dinerstein, E., and G. F. McCracken. 1990. Endangered greater one-horned rhinoceros carry high levels of genetic variation. Conservation Biology 4:417-422.

Dobson, A. P. 1999. Introduction: genetics and conservation biology. Pages xiii-xviii in L. F. Landweber and A. P. Dobson, editors. Genetics and the extinction of species. Princeton University Press, Princeton, New Jersey, USA.

Dobson, A. P., G. M. Mace, J. Poole, and R. A. Brett. 1992. Conservation biology: the ecology and genetics of endangered species. Pages 405-430 in R. J. Berry, T. J. Crawford, and G. M. Hewitt, editors. Genes in ecology. Blackwell, Oxford, UK.

Ebert, D., C. Haag, M. Kirkpatrick, M. Riek, J. W. Hottinger, and V. I. Pajunen. 2002. A selective advantage to immigrant genes in a Daphnia metapopulation. Science 295:485-488.

Falconer, D. S., and T. F. C. Mackay. 1996. Introduction to quantitative genetics. Fourth edition. Longman, Harlow, UK.

Ferson, S. 1994. RAMAS Stage: generalized stage-based modeling for population dynamics. Applied Biomathematics, Setauket, New York, USA.

Fiedler, P. L. 1987. Life history and population dynamics of rare and common Mariposa lilies (Calochortus Pursh: Liliaceae). Journal of Ecology 75:977-995.

Frankel, O. H., and M. E. Soulé. 1981. Conservation and evolution. Cambridge University Press, Cambridge, UK.

Frankham, R. 1995a. Conservation genetics. Annual Review of Genetics 29:305-327.

Frankham, R. 1995b. Inbreeding and extinction: a threshold effect. Conservation Biology 9:792-799.

Frankham, R. 1996. Relationship of genetic variation to population size in wildlife. Conservation Biology 10:1500-1508.

Frankham, R. 1998. Inbreeding and extinction: island populations. Conservation Biology 12:665-675.

Frankham, R. 2000. Genetics and conservation: commentary on Elgar and Clode. Australian Biologist 13:45-54.

Frankham, R., D. A. Briscoe, and J. D. Ballou. 2002. Introduction to conservation genetics. Cambridge University Press, New York, New York, USA.

Frankham, R., D. M. Gilligan, D. R. Morris, and D. A. Briscoe. 2001. Inbreeding and extinction: effects of purging. Conservation Genetics 2:279-284.

Gilpin, M. E., and M. E. Soulé. 1986. Minimum viable populations: processes of species extinction. Pages 19-34 in M. E. Soulé, editor. Conservation biology: the science of scarcity and diversity. Sinauer, Sunderland, Massachusetts, USA.

Ginzburg, L. R., S. Ferson, and H. R. Akçakaya. 1990. Reconstructibility of density dependence and the conservative assessment of extinction risks. Conservation Biology 4:63-70.

Haig, S. M., and J. C. Avise. 1996. Avian conservation genetics. Pages 160-189 in J. C. Avise and J. L. Hamrick, editors. Conservation genetics: case histories from nature. Chapman and Hall, New York, New York, USA.

Hedrick, P. W., and S. T. Kalinowski. 2000. Inbreeding depression in conservation biology. Annual Review of Ecology and Systematics 31:139-162.

Husband, B. C., and D. W. Schemske. 1996. Evolution of timing and magnitude of inbreeding depression in plants. Evolution 50:54-70.

Husband, B. C., and D. W. Schemske. 1997. The effect of inbreeding on diploid and tetraploid populations of Epilobium augustifolium (Onagraceae). Evolution 51:737-746.

International Union for Conservation of Nature and Natural Resources. 2000. IUCN red list of threatened species. International Union for Conservation of Nature and Natural Resources, Gland, Switzerland.

Kaiya, Z., S. Ellis, M. Leatherwood, M. Bruford, and U. S. Seal. 1994. Baiji (Lipotes vexillifer) population and habitat viability assessment report. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Kjos, C. O., O. Byers, P. M. Miller, J. Borovansky, and U. S. Seal. 1998. Population and habitat viability assessment (PHVA) for the winged mapleleaf mussel (Quadrula fragosa). Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Kushlan, J. A., and T. Jacobsen. 1990. Environmental variability and the reproductive success of Everglades alligators. Journal of Herpetology 24:176-184.

Lacy, R. C., N. R. Flesness, and U. S. Seal. 1989. Puerto Rican parrot (Amazona vittata) population viability analysis July 30, 1989. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Lande, R. 1988. Genetics and demography in biological conservation. Science 241:1455-1460.

Lande, R. 1995. Mutation and conservation. Conservation Biology 9:782-791.

Lynch, M., and B. Walsh. 1998. Genetics and analysis of quantitative traits. Sinauer, Sunderland, Massachusetts, USA.

Madsen, T., R. Shine, M. Olsson, and H. Wittzell. 1999. Restoration of an inbred adder population. Nature 402:34-35.

Mangel, M., and C. Tier. 1994. 4 facts every conservation biologist should know about persistence. Ecology 75:607-614.

Maschinski, J., R. Frye, and S. Rutman. 1997. Demography and population viability of an endangered plant species before and after protection from trampling. Conservation Biology 11:990-999.

Matsuda, H., Y. Takenaka, T. Yahara, and Y. Uozumi. 1998. Extinction risk assessment of declining wild populations: the case of the southern bluefin tuna. Researches on Population Ecology 40:271-278.

May, R. M. 1995. The cheetah controversy. Nature 374:309-310.

Menges, E. S. 1992. Stochastic modeling of extinction in plant populations. Pages 253-275 in P. L. Fiedler and S. K. Jain, editors. Conservation biology: the theory and practice of nature conservation preservation and management. Chapman and Hall, New York, New York, USA.

Menges, E. S. 2000. Population viability analyses in plants: challenges and opportunities. Trends in Ecology and Evolution 15:51-56.

Miller, P. M., and P. W. Hedrick. 2001. Purging of inbreeding depression and fitness declines in bottlenecked populations of Drosophila melanogaster. Journal of Evolutionary Biology 14:595-601.

Miller, P. M., and R. C. Lacy. 1999. VORTEX: a stochastic simulation of the extinction process; version 8 user's manual. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Mills, L. S., and P. E. Smouse. 1994. Demographic consequences of inbreeding in remnant populations. American Naturalist 144:412-431.

Murphy, D. D., K. E. Freas, and S. B. Weiss. 1990. An environment-metapopulation approach to population viability analysis for a threatened invertebrate. Conservation Biology 4:41-51.

Nevo, E., H. C. Dessauer, and K. C. Chuang. 1975. Genetic variation as a test of natural selection. Proceedings of the National Academy of Sciences 72:2145-2149.

Newman, D., and D. Pilson. 1997. Increased probability of extinction due to decreased genetic effective population size: experimental populations of Clarkia pulchella. Evolution 51:354-362.

Oostermeijer, J. G. B. 2000. Population viability analysis of the rare Gentiana pneumonanthe: the importance of genetics, demography and reproductive biology. Pages 313-334 in A. G. Young and G. M. Clarke, editors. Genetics, demography and viability of fragmented populations. Cambridge University Press, Cambridge, UK.

Pucek, Z., U. S. Seal, and P. M. Miller. 1996. Population and habitat viability assessment for the European bison (Bison bonasus). Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Ralls, K., J. D. Ballou, and A. Templeton. 1988. Estimates of lethal equivalents and the cost of inbreeding in mammals. Conservation Biology 2:185-193.

Reed, D. H., and R. Frankham. 2002. Correlation between fitness and genetic diversity. Conservation Biology 16, in press.

Ryan, B. F., B. L. Joiner, and T. A. Ryan. 1994. MINITAB handbook. Third edition. Duxby Press, Belmont, California, USA.

Saccheri, I., M. Kuussaari, M. Kankare, P. Vikman, W. Fortelius, and I. Hanski. 1998. Inbreeding and extinction in a butterfly metapopulation. Nature 392:491-494.

Sæther, B. E., S. Engen, R. Lande, P. Arcese, and J. N. M. Smith. 2000. Estimating the time to extinction in an island population of song sparrows. Proceedings of the Royal Society of London. Series B: Biological Sciences 267:621-626.

SAS Institute. 2000. JMP statistics and graphics guide. SAS Institute, Cary, North Carolina, USA.

Seal, U. S. 1994a. Attwater's Prairie Chicken (Tympanuchus cupido attwateri) population and habitat viability assessment. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Seal, U. S. 1994b. Houston toad population and habitat viability assessment report. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Seal, U. S., P. Garland, D. Butler, A. Grant, and C. O'Donnell. 1991. Population viability analysis Kea (Nestor notabilis) and Kaka (Nestor meridionalis) report. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

Simmons, M. J., and J. F. Crow. 1977. Mutations affecting fitness in Drosophila populations. Annual Review of Genetics 11:47-78.

Sinclair, A. R. E. 1996. Mammal populations: fluctuation, regulation, life history theory and their implications for conservation. Pages 127-154 in R. B. Floyd, A. W. Sheppard, and P. J. De Barro, editors. Frontiers of population ecology. CSIRO, Melbourne, Australia.

Sokal, R. R., and F. J. Rohlf. 1995. Biometry: the principles and practice of statistics in biological research. Third edition. W. H. Freeman, New York, New York, USA.

Soulé, M. 1976. Allozyme variation: its determinant in space and time. Pages 60-77 in F. J. Ayala, editor. Molecular evolution. Sinauer, Sunderland, Massachusetts, USA.

Tanaka, Y. 2000. Extinction of populations by inbreeding depression under stochastic environments. Population Ecology 42:55-62.

Taylor, A. C., W. B. Sherwin, and R. K. Wayne. 1994. Genetic variation of microsatellite loci in a bottlenecked species: the northern hairy-nosed wombat (Lasiorhinus krefftii). Molecular Ecology 3:277-290.

van Noordwijk, A. J. 1994. The interaction of inbreeding depression and environmental stochasticity in the risk of extinction of small populations. Pages 131-146 in V. Loeschcke, J. Tomiuk, and S. K. Jain, editors. Conservation genetics. Birkhäuser Verlag, Basel, Switzerland.

Vrijenhoek, R. C. 1994. Genetic diversity and fitness in small populations. Pages 37-53 in V. Loeschcke, J. Tomiuk, and S. K. Jain, editors. Conservation genetics. Birkhäuser Verlag, Basel, Switzerland.

Westemeier, R. L., J. D. Brawn, S. A. Simpson, T. L. Esker, R. W. Jansen, J. W. Walk, E. L. Kershner, J. L. Bouzat, and K. N. Paige. 1998. Tracking the long-term decline and recovery of an isolated population. Science 282:1695-1698.

Werikhe, S., L. Macfie, N. Rosen, and P. M. Miller. 1997. Can the mountain gorilla survive? Population and habitat viability assessment workshop for Gorilla gorilla beringei. Conservation Breeding Specialist Group, Apple Valley, Minnesota, USA.

World Conservation Monitoring Centre. 1992. Global biodiversity: status of the Earth's living resources. Chapman and Hall, London, UK.

Young, T. P. 1994. Natural die-offs of large mammals: implications for conservation. Conservation Biology 8:410-418.

Home | Archives | About | Login | Submissions | Notify | Contact | Search