Using the Species–Area Relationship to Set Baseline Targets for Conservation

Philip Desmet¹ and Richard Cowling²

• Abstract
• Introduction
• Methods
  • Study area
  • Estimating z-values for selected Succulent Karoo vegetation types
  • Extrapolating z-values to all Succulent Karoo vegetation types
• Results
  • Estimating z-values for vegetation types with sufficient survey data
  • Extrapolating z-values to vegetation types with insufficient data
  • Calculating conservation targets from z-values
• Discussion
  • Is 10% enough?
  • Assumptions of the power model
  • Limitations of using z-values to set targets
  • Which estimator?
  • Further sources of error
  • Extrapolating z-values
  • General
• Responses to this Article
• Acknowledgments
• Literature Cited

This paper demonstrates how the power form of the Species–Area Relationship (SAR) can be used to set conservation targets for land classes using biodiversity survey data. The log-transformation of the power model is a straight line; therefore, if one knows the average number of species recorded per survey site and can estimate the true species number present in the land class, using EstimateS software, it is possible to calculate the slope of the curve, or z-value. The z-value is the exponent in the power model and it can then be used to estimate the proportion of area required to represent a given proportion of species present in any land class. This application of the SAR is explored using phytosociological relevé data from South Africa’s Succulent Karoo biome. We also provide suggestions for extrapolating the estimated z-values to other land classes within a bioregion that lack sufficient survey data, using the relationship between z-values and remotely determined landscape variables such as habitat diversity (topographic diversity) and geographic location (latitude and longitude). The SAR predicts that for most Succulent Karoo vegetation types a conservation target of 10% of the land area would not be sufficient to conserve the majority of species. We also demonstrate that not all land classes are equal from a plant biodiversity perspective, so applying one target to all land classes in a region will lead to significant gaps and inefficiencies in any reserve network based on this universal target.

KEY WORDS: conservation planning, land classes, plant diversity, power model, South Africa, species–area relationship, Succulent Karoo, targets, vegetation types.

Published: November 18, 2004

Targets are an integral part of contemporary conservation planning, implementation, and monitoring. Systematic conservation planning is dependent on explicitness, accountability, and defensibility in identifying priority conservation areas (Margules and Pressey 2000). Conservation targets underpin this process by providing a clear purpose for conservation decisions, lending them accountability and defensibility (Pressey et al. 2003). Targets are basically quantitative interpretations of broad conservation goals that are established in policy by experts, implementing agencies, or other stakeholders (Cowling et al. 1999b, Margules and Pressey 2000, Pressey et al. 2003). For example, an agency may specify that it wishes to conserve at least 10% of each vegetation type and three populations of endangered species within its jurisdiction. Consequently, targets also provide a benchmark against which to measure the success of conservation action.

Conservation targets can be divided into two broad categories based on the scale of biodiversity surrogate targeted (Noss 1996, Pressey et al. 2003). Coarse-filter approaches set targets for features such as vegetation types, ecosystems, or land classes. Fine-filter approaches use species or populations as the focal feature for conservation action (Noss 1996). Although both approaches are complementary, for most regions limitations in species distribution data sets obligate the use of coarse-filter surrogates (Lombard et al. 2003; P. Desmet, A. Lombard, and A. Cowling, unpublished manuscript).

Vegetation or land-class maps have the advantage of covering the entire landscape, thereby eliminating the inherent spatial and taxonomic bias of species data sets (Lombard et al. 2003, Pressey et al. 2003; P. Desmet, A. Lombard, and A. Cowling, unpublished manuscript). There are limitations with using such maps. Firstly, reserve selection using the coarse-filter approach is likely to protect many species yet to be discovered or for which records are deficient. However, unless complementary fine-filter information is incorporated in the process, other species, especially rarer ones, are likely to be missed (Kirkpatrick and Brown 1994, Lombard et al. 2003; P. Desmet, A. Lombard, and A. Cowling, unpublished manuscript). Secondly, the spatial, land-class compositional, or process requirements of certain species are unlikely to be satisfied unless they are specifically targeted (Pressey et al. 2003). Such taxa have been referred to as “focal species” (Lambeck 1997, Boshoff and Kerley 1999, Noss et al. 1999, Boshoff et al. 2001) or “landscape species” (Sanderson et al. 2002). These are essentially an alternative approach to interpreting the “umbrella” or “keystone” species concepts (Bond 1993, Mills et al. 1993, Launer et al. 1994, Fleisman et al. 2000). Thirdly, land classes do not explicitly target natural processes (Pressey et al. 2003). These need to be targeted if biodiversity is to persist (Cowling et al. 1999b, Cowling and Pressey 2001).

These problems are compounded by problems related to scale. Targets framed as percentages of countries or regions can be achieved even though they fail to protect the natural features most urgently in need of protection (Pressey et al. 2003). Large regions are heterogeneous in terms of biodiversity and potential for anthropogenic transformation. Conservation areas have often been relegated to the least useable portions of regions, thereby avoiding areas where past impacts on biodiversity have been greatest and future threats are most serious (Noss et al. 1999, Pressey et al. 2000, Scott et al. 2001). This is true even of regions with formal protection overall equal to or greater than 10% (Armesto et al. 1998, Barnard et al. 1998, Soulé and Sanjayan 1998, Pressey et al. 2000, Rouget et al. 2003). Also, coarse-scale maps do not capture all possible land-class combinations, so even if vulnerability over the whole area is low, certain landscape biodiversity features (e.g., rare vegetation types or habitats) can fall through the cracks (P. Desmet, A. Lombard, and A. Cowling, unpublished manuscript). These issues can be addressed by mapping at finer scales and with improved mapping techniques (Ferrier 2002; P. Desmet, A. Lombard, and A. Cowling, unpublished manuscript). Targeting better mapped land types with classes that are more homogeneous, in terms of biodiversity and land use potential, limits the potential for conservation action to miss capturing all biodiversity (Bedward et al. 1992).

Considering these limitations, it must be accepted that, for the majority of areas on this planet, land-class maps of some sort will be the primary biodiversity feature used for conservation and land-use planning. Thus, how can biologically meaningful quantitative conservation targets for land classes be set? Although there are some studies dealing with a range of species (Margules et al. 1988, Saetersdal et al. 1993, Travaini et al. 1997), minimum viable population (Nunney and Campbell 1993, Boshoff et al. 2001, Burgman et al. 2001), meta population (Lindenmayer and Lacy 1995), genetic diversity (Lacy 1997, Ferguson et al. 1998), community (Prins et al. 1998), habitat (Turner et al. 1999, Calkin et al. 2002), or ecosystem (Turner et al. 1992, Noss 1996) targets, there is generally a paucity of work dealing specifically with targets for land classes.

The widely used 10% target, recommended by IUCN (International Union for the Conservation of Nature), when applied to land classes, implies that all are equal in terms of their species diversity, abundance, and distribution. This is certainly not the case. More questionable though, is the biological foundation for this target. Despite the potential arbitrariness of this target (Soulé and Sanjayan 1998, Pressey et al. 2003), the origin is partly founded in the original work on the species–area relationship. A general “rule of thumb” first noted by Darlington (1957) and developed from early observations of species–area relationships was that a 10-fold decrease in area resulted in a twofold decrease in species, or, alternatively, 10% of an area would conserve 50% of the species (Diamond and May 1976). Even if at some point this observation influenced the conception of the IUCN 10% target at the World Parks Congress in Caracas in 1993, the question arises as to whether saving 50% of the planet’s terrestrial species is really adequate. General consensus in the literature is that 10% of area is not sufficient to represent the majority of biodiversity, assuming that the remainder of the landscape is cleared or not conserved (Soulé and Sanjayan 1998, Rodrigues and Gaston 2001).

Is it possible to set ecologically meaningful targets for land classes? In an attempt to address this question, this paper returns to one of ecology’s oldest observations, the species–area relationship (SAR), to find answers.

“You will find more species if you sample a larger area” (Rosenzweig 1995). This could also be stated as follows: “you will conserve more species if you conserve a larger area.” This observation forms the basis of the SAR. Patterns in the SAR are well explored in the ecological literature across a range of spatial and temporal scales (Rosenzweig 1995, Lomolino 2000, Knowles 2001, Lomolino and Weiser 2001, Collins et al. 2002, Haila 2002). Attempts have been made to develop a functional understanding of the SAR (e.g., Harte et al. 1999b). Although there is as yet no widely accepted ecological theory to explain the relationship, the basic pattern is real. Many mathematical models can and have been used to describe the SAR (Lomolino 2000), but the power relationship or Arrhenius equation is probably the most popular in the literature (Rosenzweig 1995):

(1)

In this relationship, k is a scaling factor that relates to the sample size used (Rosenzweig 1995, Lomolino 2000) and it can be ignored when comparing proportions or percentages of area and species (Vreugdenhil et al. 2003). The meaning of k is debatable (Gould 1979, Lomolino 2000, 2001), but we will not discuss this here. The rate at which species are encountered in a system is described by the parameter z (Rosenzweig 1995, Lomolino 2000). The SAR has been applied to a host of questions in ecology. Those with a direct conservation angle range from the “Single Large Or Several Small” debate (Diamond and May 1976, Bond et al. 1988, Deshaye and Morisse 1989, Cowling and Bond 1991) to predicting the loss of species from fragmented landscapes (Tilman et al. 1994, Kemper et al. 1999, Cornelius et al. 2000, Miller and Cale 2000, Magura et al. 2001, Acosta and Robertson 2002, Haila 2002, Tscharntke et al. 2002, Zurlini et al. 2002).

Fragmentation research has come very close to actually addressing the target issue by using Eq. 1 to estimate the proportion of species lost, given a reduction in area (Brooks et al. 1999, Kinzig and Harte 2000). However, the suitability of using the SAR to predict species loss due to habitat transformation has been questioned recently (Seabloom et al. 2002). From a conservation planning perspective, rather than asking how many species will be lost if a landscape is fragmented, the question can be turned around to ask how many species will be gained by a protected area network if more landscape is added to the network.

Diamond and May (1976) used the power equation to predict the number of species remaining if a given percentage of a landscape was transformed. If the z-value for a biota or land class is known, then by using Eq. 2 it is possible to predict the proportion of species remaining if the area is reduced by a given proportion.

(2)

Here S’ and A’ denote the proportion of species and area rather than absolute values. This equation can be reordered to address conservation targets to determine the proportion of area required to represent a given percentage of species:

(3)

For the SAR rule of thumb previously discussed (a 10-fold decrease in area equates to a twofold decrease in species) the z-value here is approximately 0.3. Using this same z-value but changing the percentage of species targeted to 75%, it follows from Eq. 3 that the percentage of the area required increases from 10% to 38%. If the species target is increased to 95%, then the area target becomes 84%! These are quite significant changes in the area required to meet this basic biodiversity target of representing each species at least once. Published z-values for biotas range between approximately 0.1 and 0.4 (Rosenzweig 1995). Although this range in the exponent is small, the nature of the power equation means that for a species target of 75%, the area target can range from 5% to 48%, respectively, for z-values from 0.1 to 0.4.

It is possible to use the SAR to set conservation targets for land classes. The method for setting this target involves estimating the area of a land class that is required to represent a given proportion of the species occurring in the land class. Thus, it remains a question of being able to calculate the z-value of the SAR for a land class. To achieve this it is necessary to generate a SAR curve based on some form of inventory data. Because the curve of the power model is a straight line in log–log space and the slope is the z-value, it is possible to calculate the z-value without generating the actual curve by using species–area data that sample larger and larger proportions of a land class. There is no need to demonstrate the relationship by fitting the power curve, because the suitability of the model is assumed a priori. For the log transformation of the power model, the slope of the curve (hence, the z-value) can be determined using the formula for calculating the slope of a straight line:

(4)

Here z is the slope of the straight line, y₂ = log(total number of species in a land class); y₁ = log(average number of species per survey sample); x₂ = log(total area of land class); and, x₁ = log(average area of samples). When using inventory data, three of these variables are known; all that remains is to estimate the total number of species that occur in the vegetation type. Several nonparametric estimator functions are available for estimating the true number of species in an area based on a set of random samples (Colwell and Coddington 1995, Colwell 1997).

In this paper, phytosociological survey data are used to calculate the z-values for land classes (Succulent Karoo biome vegetation types) by estimating the true number of species per vegetation type using EstimateS software (Colwell 1997). Firstly, z-values for vegetation types with sufficient survey sites to allow for meaningful estimates to be made are calculated. Following from this, observed z-values are extrapolated to other vegetation types in the Succulent Karoo that do not have survey data. This is achieved by relating known z-values to landscape physical properties that act as surrogates for geographic species turnover and habitat diversity. Finally, some generalizations about land-class characteristics are made that can be applied to other conservation situations in which suitable survey data are lacking.

Study area

The Succulent Karoo biome covers an area of approximately 116 000 km² located in the southwestern corner of southern Africa (Fig. 1). It forms the arid ecotone (rainfall <350 mm/yr) between the winter-rainfall Fynbos biome and the summer-rainfall biomes of the region (Cowling et al. 1999a, Dean and Milton 1999). Floristically, it forms part of the Cape Floral Kingdom (J. Born, H. P. Linder, and P. Desmet, unpublished data). The hallmark of the Succulent Karoo is its exceptionally diverse and endemic-rich flora, especially succulents and bulbs. The biome is home to 6356 plant species, 40% of which are endemic and 936 (17%) of which are Red Data Listed (Driver et al. 2003). In addition to its floral diversity, the biome is a center of diversity for reptiles and many groups of invertebrates. The Succulent Karoo biome is one of 25 internationally recognized biodiversity hotspots and is the world’s only arid hotspot (Mittermeier et al. 1998). However, only 3.5% is formally conserved, and the biome’s biodiversity is under pressure from a range of human impacts, especially mining, crop agriculture, ostrich farming, overgrazing, illegal collection of fauna and flora, and anthropogenic climate change (Driver et al. 2003). Hence the urgency to address the question of conservation targets.

Fig. 1. The location of the study area on the southwestern corner of the African continent.

Estimating z-values for selected Succulent Karoo vegetation types

Phytosociological relevé data from the Succulent Karoo biome were used to estimate true species numbers for Succulent Karoo vegetation types. The relevé database contained 5491 geo-referenced survey sites from 25 different studies conducted in the biome over the last 20 years. The Succulent Karoo was expertly classified and mapped into 132 vegetation types (Driver et al. 2003). Each relevé was assigned to a vegetation type based on its geographic location. In total, 42 vegetation types, each with more than 30 relevés, were used for the analyses. The 30-sample limit was determined in exploratory analyses as being the smallest average number of samples for which the standard deviation of the final estimate was less than 5% of the estimate.

The software package EstimateS (Colwell 1997) was used to generate estimates of the total number of species present in each vegetation type based on the samples of survey plots. EstimateS provides the user with 10 nonparametric statistical functions to estimate the true number of species based on species incidence in a sample of survey sites. These estimators are discussed in Colwell and Coddington (1995). Only seven estimators (ACE, ICE, Chao1, Chao2, Jack-knife1, Jack-knife2, and Bootstrap) were used in the comparative analyses, as the others (Michaelis-Menten runs, Michaelis-Menten means, and Cole) have not been widely tested for this purpose in the literature (Brose 2002, Herzog et al. 2002, Chiarucci et al. 2003, Petersen et al. 2003, Turnipseed et al. 2003). The estimated true species number was used in Eq. 4 to calculate the z-value of the SAR for each vegetation type.

Extrapolating z-values to all Succulent Karoo vegetation types

The ultimate goal of this exercise is to generate conservation targets for all land classes within a biome or planning domain. The problem faced in the Succulent Karoo, as well as most of the rest of the world, is that there are inadequate survey data for all land classes. For this Succulent Karoo example, 42 out of 132 vegetation types had 30 or more survey sites, with only nine having more than 100 relevés. Therefore it is necessary to extrapolate z-values (or targets) to all vegetation types within a biogeographic province based on an observed relationship between the calculated z-values for vegetation types or land classes and some remotely measurable land-class properties that could explain macro patterns of diversity.

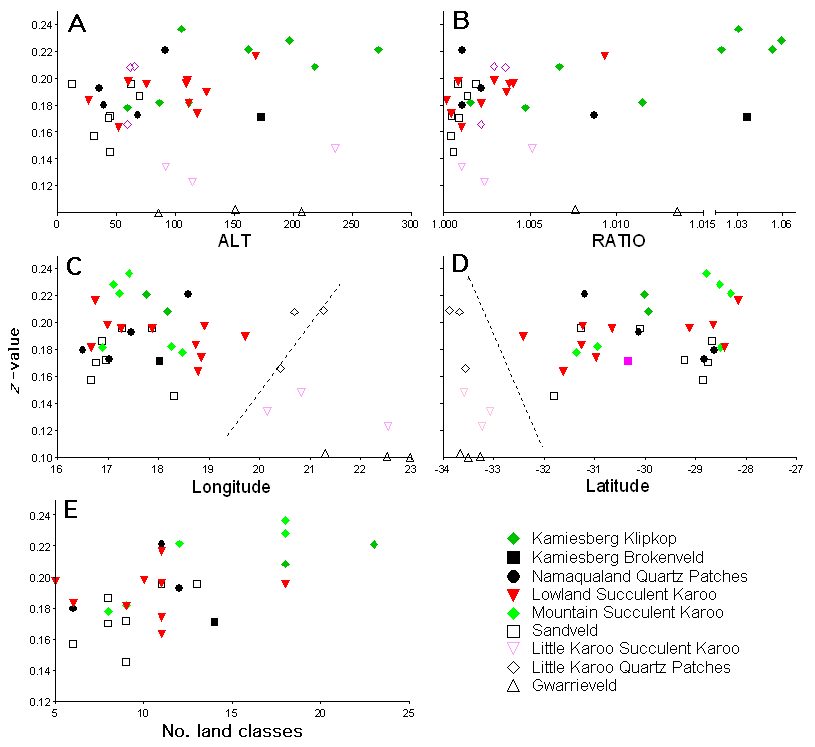
The effect of area has already been accounted for in the z-value. Species diversity also relates strongly to habitat diversity (Rosenzweig 1995). Therefore, it makes sense to introduce a variable that can act as a surrogate for habitat diversity. Z-values are related to two independent measures of land-class habitat diversity. The first is a simplistic measure of topographic diversity summarized in two ways: (1) the standard deviation of the mean altitude for a vegetation type as determined from a 100-m grid cell resolution digital elevation model; and (2) the ratio of volumetric to planimetric surface area per vegetation type, determined from the same elevation model. The hypothesis is that more topographically heterogeneous land classes would have more habitats and, consequently, would support more species per unit area and have higher z-values.

The second measure of habitat diversity is a count of the number of ecological land classes present within each vegetation type. Eecological zones were developed using a generalized dissimilarity modeling technique discussed in Ferrier (2002) and applied by S. Ferrier, G. Manion, and P. Desmet (unpublished manuscript) for the Namaqualand region of the Succulent Karoo. Each zone is determined as a function of remotely determined topographic, edaphic, and climatic variables scaled according to observed patterns of plant diversity. Each zone can be considered environmentally and biologically homogeneous relative to other zones; thus a count of the number of zones represented in a vegetation type can be regarded as an alternative, albeit crude, measure of habitat diversity.

In addition to the three habitat or beta diversity variables, latitude and longitude were introduced as geographic or gamma diversity variables. For the analyses, the geographic centroid of each vegetation type was used. These variables are useful at the landscape scale, because patterns of gamma diversity relate strongly to distance between areas (Ferrier et al. 2002).

To develop the relationships between z-values and the landscape variables, the 42 vegetation types were grouped into eight higher order vegetation-type categories, i.e., categories between the lower level of vegetation type and upper level of biome (Table 1). The groups were based on known biogeographic and physiognomic similarities in vegetation types. Regression models relating z-values to the environmental variables were built using linear, nonlinear, and generalized additive modeling methods. The S-Plus statistical package (http://www.mathsoft.com/splus/) was used to perform analyses.

Table 1. The classification of vegetation types into higher order vegetation categories or groups. Vegetation types in each category were used to develop regression models relating observed z-values for vegetation types within each category to remotely determined landscape variables. Vegetation Category Vegetation type   Bushmanland Nama Karoo Bushmanland Arid Grassland, Karas Upland Nama Karoo   Gwarrieveld Eastern Little Karoo, Vanwyksdorp Gwarrieveld, Western Spekboomveld   Kamiesberg Brokenveld Kamiesberg Mountain Brokenveld   Little Karoo Quartz-patches Anysberg Quartz Patches, Langeberg Quartz Patches, Warmwaterberg Quartz Patches   Little Karoo Succulent Karoo Prince Albert Succulent Karoo, Southern Tanqua Karoo, Western Little Karoo   Namaqualand Quartz-patches Alexander Bay Gravel Patches, Eastern Bushmanland Quartz and Gravel Patches, Knersvlakte Quartzfields, Lekkersing Quartz Patches, Riethuis Quartzfields   Namaqualand Succulent Karoo Central Knersvlakte Lowland Succulent Karoo, Central Richtersveld Succulent Karoo, Knersvlakte Shales, Namaqualand Klipkoppe, Namaqualand Klipkoppe Flats, Namaqualand Lowland Succulent Karoo, Northern Knersvlakte Lowland Succulent Karoo, Northern Richtersveld Lowland Succulent Karoo, Nuwerus Quartzite Succulent Karoo, Richtersberg Mountain Desert, Rooiberg Quartzite Succulent Karoo, Southeastern Richtersveld Quartzites, Southern Knersvlakte Lowland Succulent Karoo, Southern Richtersveld Lowland Succulent Karoo, Tanqua Karoo, Upper Annisvlakte Succulent Karoo, West Gariep Desert, West Gariep Lowlands   Sandveld Lamberts Bay Strandveld, Namaqualand Coastal Dunes, Namaqualand Red Sand Plains, Namaqualand Southern Strandveld, Northern Richtersveld Yellow Dunes, Richtersveld Red Dunes, Richtersveld White Dunes

Estimating z-values for vegetation types with sufficient survey data

Estimates of true species number for Succulent Karoo vegetation types are presented in Table 2. As expected, there is considerable variation in the predictions of the different estimators. For this analysis, we decided to use only the Bootstrap estimator to calculate the z-value rather than, for example, using a mean of all estimators. Exploratory analyses using model data indicated that this estimator provided the most consistent estimates under a range of modeled data conditions (P. Desmet, unpublished data). The Bootstrap estimator is consistently the lowest of the seven estimates of true species number (Table 2). This estimate is, for the most part, within or close to the lower standard deviation limit of the other estimates.

Table 2. Estimates of true species number for 42 Succulent Karoo vegetation types. Values are rounded to the nearest whole number. Only mean values for ACE, ICE, Jack-knife 2 and Bootstrap are calculated by EstimateS. Values for number of species per plot and Chao1, Chao2, and Jack1 are means (with 1 SD in parentheses). The z-value was calculated using the Bootstrap estimator. Survey data properties Estimates Estimate range           Succulent Karoo vegetation types No. rel- evés Spp. per  plot  No. spp.  obs.   Indi-  vid- uals  Single-  tons Double- tons  ACE   ICE   Chao  1  Chao  2  Jack  1  Jack  2  Boot-  strap  Esti-  mate range  Mean  esti- mate  Range  (% of mean) z-value est. Alexander Bay    Gravel Patches 73 12 (5) 145 855 54 18 209 210 220 (31) 220 (31) 198 (11) 234 168 66 208 32 0.18 Anysberg Quartz    Patches 153 21 (13) 218 2765 44 23 249 249 257 (17) 257 917) 262 (8) 283 239 44 257 17 0.166 Bushmanland    Arid Grassland 59 6 (5) 151 443 78 27 287 290 258 (35) 258 (35) 228 (24) 277 184 106 255 42 0.184 Central Knersvlakte Low-    land Succulent Karoo 35 7 (5) 84 252 42 8 137 139 180 (53) 180 (53) 125 (12) 157 101 79 146 54 0.183 Central Richtersveld    Succulent Karoo 163 12 (9) 394 1911 170 56 624 626 646 (55) 646 (55) 563 (27) 676 466 210 607 35 0.228 Eastern Bushmanland    Quartz and Gravel Patches 66 50 (44) 320 2802 63 30 363 365 383 (22) 383 (22) 382 (24) 414 349 65 377 17 0.162 Eastern Little Karoo 30 15 (3) 58 466 14 10 68 68 66 (7) 66 (7) 72 (4) 76 65 11 69 16 0.099 Kamiesberg Mountain    Brokenveld 49 21 (9) 313 995 138 66 492 497 454 (33) 454 (33) 448 (25) 519 374 145 463 31 0.171 Karas Upland Nama    Karoo 31 9 (5) 80 308 27 16 104 105 101 (11) 101 (11) 106 (7) 117 92 25 104 24 0.137 Knersvlakte Quartzfields 477 10 (8) 311 4101 84 45 393 394 387 (23) 387 (23) 395 (13) 434 350 84 391 21 0.221 Knersvlakte Shales 61 7 (3) 130 434 55 29 199 201 180 919) 180 (19) 184 (12) 210 155 55 187 29 0.197 Lamberts Bay Strandveld 312 23 (6) 175 7603 76 16 364 364 343 (63) 343 (63) 251 (46) 310 205 159 311 51 0.145 Langeberg Quartz Patches 68 10 (8) 182 735 56 25 224 226 241 (22) 241 (22) 237 (10) 268 207 61 235 26 0.209 Lekkersing Quartz    Patches 68 9 (4) 114 582 33 28 142 142 132 (9) 132 (9) 147 (10) 152 130 22 140 16 0.172 Namaqualand Coastal    Dunes 62 15 (6) 197 925 68 36 264 266 259 (21) 259 (21) 264 (17) 295 228 67 262 26 0.172 Namaqualand Klipkoppe 282 13 (11) 640 3801 251 104 939 940 939 (51) 939 (51) 890 (35) 1036 750 286 919 31 0.221 Namaqualand Klipkoppe    Flats 150 8 (6) 244 1247 106 35 384 385 399 (43) 399 (43) 349 (33) 420 289 131 375 35 0.208 Namaqualand Lowland    Succulent Karoo 53 16 (14) 358 932 157 78 524 529 513 (33) 513 (33) 512 (24) 590 428 162 516 31 0.196 Namaqualand Red Sand    Plains 151 24 (16) 603 3164 249 88 923 926 950 (61) 950 (61) 850 (48) 1010 709 301 903 33 0.195 Namaqualand Southern    Strandveld 48 15 (11) 186 712 66 39 254 256 240 (18) 240 (18) 251 914) 277 216 61 248 25 0.195 Northern Knersvlakte Low-    land Succulent Karoo 62 6 (3) 94 424 36 14 135 136 136 (21) 136 (21) 129 (9) 151 110 41 133 31 0.174 Northern Richtersveld Low-    land Succulent Karoo 70 10 (6) 147 586 75 21 268 270 273 (44) 273 (44) 221 (20) 274 178 96 251 38 0.198 Northern Richtersveld    Yellow Dunes 130 11 (6) 138 1450 51 15 194 195 218 (34) 218 (34) 189 (12) 224 160 64 200 32 0.17 Nuwerus Quartzite    Succulent Karoo 35 42 (32) 287 1444 61 41 323 325 331 (15) 331 (15) 346 (15) 366 316 50 334 15 0.182 Prince Albert Succulent    Karoo 137 12 (4) 94 1726 8 8 97 97 97 (4) 97 (4) 102 (3) 102 98 5 99 5 0.123 Richtersberg Mountain    Desert 75 8 (5) 207 646 103 31 358 361 371 (47) 371 (47) 309 (22) 379 250 129 343 38 0.221 Richtersveld Red Dunes 98 7 (2) 90 706 44 17 161 161 143 (23) 143 (23) 134 (14) 160 109 52 144 36 0.186 Richtersveld White Dunes 51 15 (7) 122 815 30 16 144 145 148 (14) 148 (14) 151 (6) 165 136 29 148 20 0.157 Riethuis Quartzfields 51 15 (11) 205 615 92 45 330 334 296 (26) 296 (26) 295 (23) 341 245 96 305 31 0.193 Rooiberg Quartzite    Succulent Karoo 41 10 (6) 109 380 38 20 142 143 143 (15) 143 (15) 146 (8) 164 126 38 144 26 0.178 Southeastern Richters-    veld Quartzites 152 7 (4) 235 1244 85 27 325 325 363 (40) 363 (40) 319 (19) 377 271 106 335 32 0.237 Southern Knersvlakte Low-    land Succulent Karoo 55 8 (3) 98 432 32 16 124 125 127 (15) 127 (15) 129 (7) 145 113 32 127 25 0.164 Southern Richtersveld Low-    land Succulent Karoo 41 6 (7) 116 298 46 31 164 165 148 (13) 148 (13) 161 (13) 176 138 38 157 24 0.196 Southern Tanqua Karoo 120 17 (6) 133 1849 31 21 162 162 154 (11) 154 (11) 164 (6) 174 148 26 160 16 0.134 Tanqua Karoo 272 11 (6) 299 3101 89 44 382 383 386 (25) 386 (25) 388 (14) 433 339 94 385 24 0.19 Upper Annisvlakte    Succulent Karoo 36 10 (5) 114 348 60 19 216 220 203 (34) 203 (34) 172 (17) 212 139 81 195 42 0.182 Vanwyksdorp    Gwarrieveld 47 31 (10) 143 1389 38 14 175 176 190 (23) 190 (23) 180 (12) 203 159 44 182 24 0.103 Warmwaterberg Quartz    Patches 122 8 (7) 177 1254 46 21 212 213 224 (20) 224 (20) 223 (9) 247 198 49 220 22 0.208 West Gariep Desert 313 9 (6) 295 3099 64 46 341 341 338 (15) 338 (15) 359 (12) 377 326 51 346 15 0.217 West Gariep Lowlands 63 9 (6) 121 499 51 19 186 187 185 (26) 185 (26) 171 (13) 202 143 59 180 33 0.181 Western Little Karoo 162 25 (11) 291 4111 66 40 342 343 343 (18) 343 (18) 357 (12) 383 322 61 348 18 0.148 Western Spekboomveld 35 29 (9) 142 1019 35 12 168 170 188 (24) 188 (24) 176 (12) 198 157 41 178 23 0.101

The z-value was calculated for each vegetation type using Eq. 4. The average relevé size was taken to be 10 x 10 m or 100 m². Varying the relevé area by an order of magnitude (i.e., 10 to 1000 m²) changed the resultant z-value by less than 0.01%.

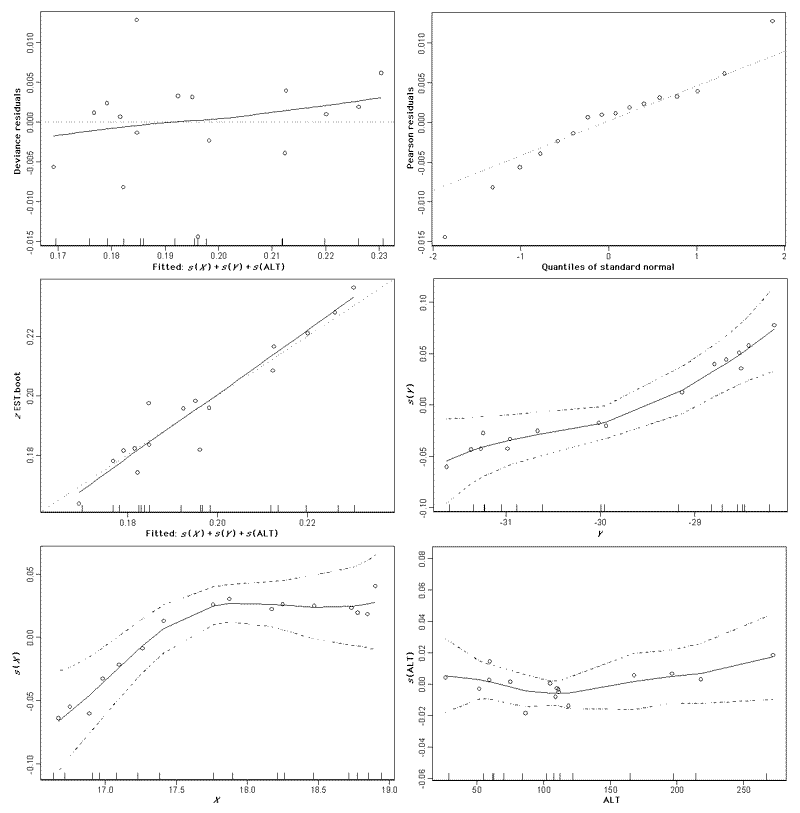
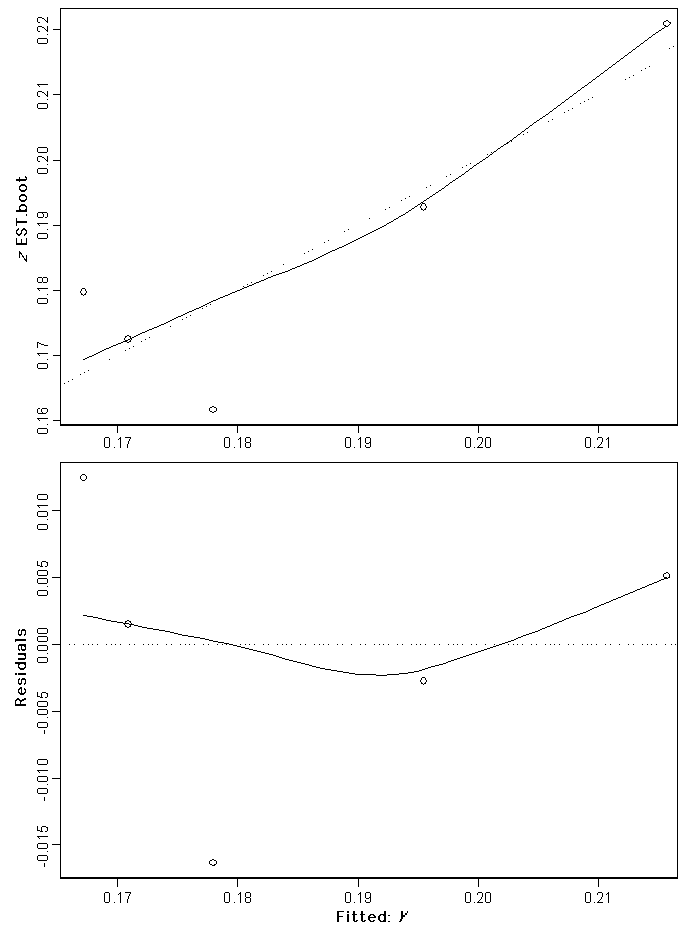
Extrapolating z-values to vegetation types with insufficient data

In order to extrapolate the observed patterns in z-values to all vegetation types in the Succulent Karoo, the z-values were related to the five landscape environmental variables (Fig. 2). In Fig. 2, the z-values are classified into the higher order vegetation categories presented in Table 1. There appear to be relationships between observed z-values per vegetation type category and the landscape variables examined. Regression models were built for the Namaqualand Succulent Karoo (Fig. 3); Namaqualand quartz patches (Fig. 4 and Fig. 5); and Sandveld (Fig. 6) vegetation categories (see Appendix 1). These were the only models that were significant, given the number of data points (i.e., vegetation types with calculated z-values) available fore each model. For all three cases, the basic model used to extrapolate values expresses the z-value, firstly, as a function of geographic location and, secondly, as a function of topographic diversity.

Fig. 2. The relationship between estimated z-values and: (A) the standard deviation of mean vegetation type altitude (ALT); (B) the ratio between planimetric and surface area of each vegetation type (RATIO); (C) longitude of vegetation type centroid; (D) latitude of vegetation type centroid; and (E) the number of modelled land classes per vegetation type. The Namaqualand and Little Karoo regions of the Succulent Karoo are separated by a dashed line in the longitude (C, Namaqualand to the left) and latitude (D, Namaqualand to the right) graphs. For this figure only the Namaqualand Succulent Karoo vegetation group has been divided into three subgroups: Kamiesberg Klipkop, Lowland Succulent Karoo, and Mountain Succulent Karoo.

Fig. 3. Regression model outputs for the Namaqualand Succulent Karoo vegetation types group using a generalized additive model (Appendix 1).

Fig. 4. The fitted regression model (top) and residuals (bottom) for Namaqualand quartz patch vegetation types group (Appendix 1).

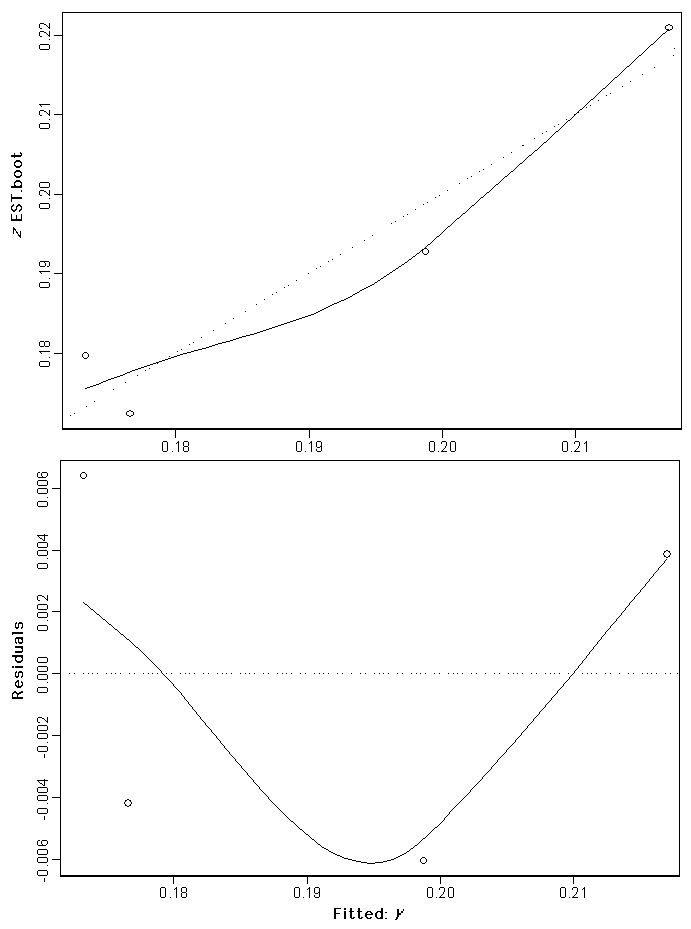
Fig. 5. The fitted regression model (top) and residuals (bottom) for the Namaqualand quartz patch vegetation types group excluding Eastern Bushmanland Quartz And Gravel Patches (Appendix 1).

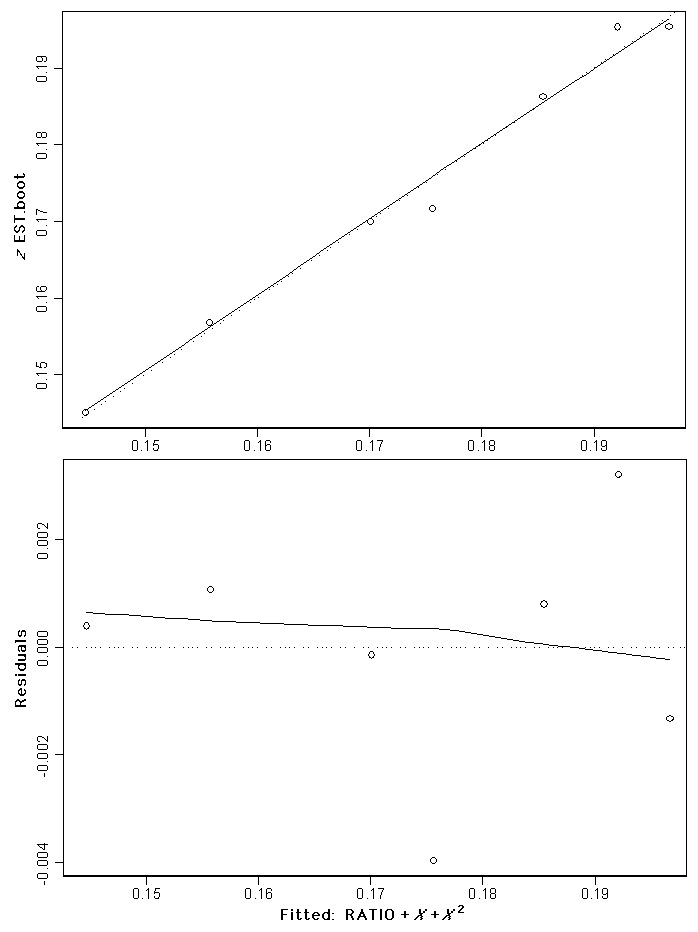
Fig. 6. The fitted regression model (top) and residuals (bottom) for the Sandveld vegetation types group (Appendix 1).

Comparing the response of z-values in the three models, it is clear that patterns of plant biodiversity within different higher order vegetation-type categories respond differently in relation to the landscape variables examined. Although geographic distance and habitat diversity are significant variables explaining the pattern in z-values, the observed pattern is different in each of the three vegetation groups. Thus, it was not possible to develop a single general model to extrapolate z-values for all Succulent Karoo vegetation types. For the remainder of vegetation types that did not fall into one of the three vegetation categories with models, we awarded the observed z-value for the geographically nearest vegetation type within their respective higher order vegetation category.

Calculating conservation targets from z-values

Conservation targets were calculated for vegetation types using Eq. 3. Examples of the range in conservation target values, expressed as the percentage of vegetation type required to represent a given percentage of plant species occurring in that vegetation type, are calculated for the observed range in z-values (,Table 3).

Table 3. Targets for Succulent Karoo vegetation types expressed as the percentage area of a vegetation type required to represent a given proportion of the total estimated number of plant species that occur in that vegetation type. Targets are calculated for the range of observed z-values and are rounded off to the nearest whole number.   Proportion of species targeted   z 0.5 0.6 0.7 0.8 0.9   0.1 1 1 3 11 35 0.125 1 2 6 17 43 0.15 1 3 9 23 50 0.175 2 5 13 28 55 0.2 3 8 17 33 59 0.225 5 10 20 37 63 0.25 6 13 24 41 66 0.3 10 18 30 48 70

If the conservation objective is to represent the majority of biodiversity (e.g., between 70% and 80% of species) within the formal reserve network, then the SAR would predict that well in excess of 10% would be required for most land classes. For the Succulent Karoo vegetation types, where a conservative average estimate of the z-value is 0.18, this would translate into a target of between 14% and 30% of the land area required to represent between 70% and 80% of the species, respectively. For the Succulent Karoo, a representation target of 75% of species was set based on regional-level discussion with stakeholders. The complete set of targets for Succulent Karoo vegetation types can be found in Driver et al. (2003).

Is 10% enough?

The approach to setting targets discussed in this paper does provide an ecological framework for testing the validity of the widely used 10% conservation target. The SAR would predict that, for most Succulent Karoo vegetation types, a conservation target of 10% of the land area would not be sufficient to conserve the majority of species. It is likely that this is the same for most land classes elsewhere on Earth. A 10% target may be valid for only the most species-poor land classes.

Another important finding of this study is that not all land classes are equal from a biodiversity perspective. Just as 10% is not enough to represent most species, applying one target to all land classes will lead to significant gaps and inefficiencies in any resultant reserve network (Soulé and Sanjayan 1998, Pressey et al. 2003).

Assumptions of the power model

The approach here assumes that the power model best describes the species–area relationship. This model rests on the assumption that species–abundance within in a land class follows a log-normal distribution (Preston 1948, May 1975, Rosenzweig 1995). It is questionable whether this assumption holds for most species. It is to be expected that as species–abundance distributions deviate from this distribution, so the difference between predicted and actual targets widens. Harte et. al. (1999a) have proposed an alternative derivation of the power model based on self-similarity in the distribution and abundance of species. This derivation does not assume a log-normal species–abundance distribution. Thus, the power model may still be valid for setting conservation targets if it is not dependent on the species–abundance distribution.

In addition, the nature of the power function means that the curve only reaches 100% of species at 100% of area. How valid this is in reality is debateable (Lomolino 2002). It is probably possible to represent 100% of species within less than 100% of area. Does this represent a breakdown in the validity of the power model as the curve approaches the asymptote, or a defect in the model as a whole? This artefact should not stop conservationists from targeting 100% of species. However, the power form of the SAR cannot be used to predict what the actual area will be for achieving this target.

Limitations of using z-values to set targets

The most important limitation of using z-values to set conservation targets is that it says nothing about where species are located in the landscape. It only provides an indication of the rate at which species are likely to be accumulated. Consequently, it says nothing about which 20% of the land class is required to represent the 75% of species being targeted. If species are distributed randomly in a land class, then reserving any 20% will capture roughly all of the predicted percentage of species targeted. Unfortunately, species are not distributed randomly and it is unlikely that the location of every species in the landscape will be known. Real-world applications of these targets will capture larger areas than those predicted by the SAR target due to inefficiencies in adding areas to a conservation network. This stresses the need for at least some species point-locality data to help guide conservation decisions.

Secondly, the z-value describes the accumulation of species based on a single occurrence of a species. A target set using z is analogous to saying, “select one occurrence of each species” in a minimum set. However, it is more than likely that numerous occurrences of common species may actually be incorporated into the notional or real system by the target. This is good, because common species often require larger populations for persistence (Lawton 1988). Also, no vegetation types in the Succulent Karoo have exclusive species complements. Consequently, the same species will be targeted in many vegetation types. Unfortunately, rare or very patchy (habitat-specific) species, i.e., the other 25% of species not targeted, are likely to be missed. Point-locality data for species that are good surrogates for this group (e.g., rare habitats) are necessary in the conservation planning process.

If the conservation goal is to select at least three occurrences of each species, then the target will have to be increased to accommodate especially rare species. How the SAR method can be used to achieve this needs to be explored.

Lastly, z-values will increase as a result of land-class fragmentation (Rosenzweig 1995). Archipelagos typically have higher z-values than mainland areas. This is generally ascribed to different rates of immigration, extinction, and in situ speciation that occur in island or naturally fragmented biotas (Diamond and May 1976, Bond et al. 1988, Brown and Dinsmore 1988, Rosenzweig 1995, Lomolino and Perault 2001, Haila 2002). Targets derived here assume that a land class is untransformed. Under anthropogenic transformation, however, a larger area than predicted by the model will be required to achieve the same species target. This is a crucial point that needs to be borne in mind when applying this approach. Species relaxation in fragmented landscapes results in a net loss in the original number of species present, as species go extinct from habitat patches over time (Brooks et al. 1999, Robinson 1999, Debinski and Holt 2000, Gonzalez 2000, Kelt 2001). This effectively increases the z-value as a larger area is required to represent the same given percentage of the original species complement. How to adapt SAR targets to landscapes under contemporary transformation needs further investigation.

Which estimator?

Probably the largest source of error in this approach lies in the estimation of the true species number for a vegetation type. There is no consensus in the literature as to which is the best estimator to use (Colwell and Coddington 1995, Chiarucci et al. 2003, Petersen et al. 2003). There is agreement, however, that the Bootstrap estimator is the most conservative (Colwell and Coddington 1995), but no consensus as to which estimator provides the best predictions (Brose 2002, Herzog et al. 2002, Chiarucci et al. 2003, Petersen et al. 2003, Turnipseed et al. 2003). In this analysis it was observed that the Bootstrap estimator was consistently the lowest estimate of the seven estimators calculated. Therefore, the estimates of z-values and targets calculated in this paper should to be regarded as conservative and probably underestimates of true targets. The rationale for using the Bootstrap technique here is based solely on the observed patterns in estimation error for modeled species data sets (P. Desmet, unpublished data). A better approach may be to use the average of several or all of the estimators. Another approach may be to calculate z-values using all estimators and then deriving a target range. This error, however, does not detract from the utility of the SAR for setting targets, but is rather a source of error in predictions of the model.

The best means of eliminating this error would be not to use the estimators to calculate the true species number, but instead to use an alternative technique for estimating z-values. Two techniques in the literature hold promise in this regard. Firstly, Harte et al. (1999b) have developed a method of calculating the SAR using species spatial-turnover data. D. P. Faith (personal communication) has proposed a method for calculating z-values using the environmental diversity index (Faith 2003). Both of these techniques can use the same inventory data, but eliminate the need to estimate true species number.

In regions where there are no survey data, but there are inventory data of some form (such as museum collections), it would be useful to explore determining z-values directly from the species–abundance distribution in the pooled inventory data for a land class. Wright (1988) showed that the z-value can be determined directly from this distribution. The assumption here would be that the number of times that a species is recorded in an inventory would be indicative of the species’ relative abundance in the land class. This would obviate the need for area-based survey sites, and would also create a novel and very important use for museum data.

As a point of clarification, the z-value cannot be calculated directly by generating a species–accumulation curve for a sample of survey sites. This curve is not a species–area curve; rather, it is a collector’s curve. A species–area curve is constructed by adding successively larger sampled areas to the data pool until one has sampled the entire land class. The accumulation of species with this progression is then plotted. Survey data are generally sampled at the same spatial scale; hence, simply generating the collector’s curve as one randomly adds sites to the data pool would result in significant errors in the z-value. In addition, the collector’s curve rarely fits the power model.

Further sources of error

Further bias arises as a result of errors in the survey data. Errors in this type of data are a perennial problem. These include sampling biases leading to uneven sampling of land classes; geo-referencing errors; omission of cryptic species; species identification errors; and data capture and archival errors. No effort is made here to control for these errors beyond the normal checks and balances, such as checking spelling, involved with collating and curating a large biological survey database.

Also, the survey data cover a range of projects that span 30 years of research in the Succulent Karoo and involve tens if not hundreds of workers. None of these projects was aimed at landscape-level biodiversity inventory, although phytosociological studies do tend to target all observed plant communities within their respective study areas. The potential for taxonomic errors is high, especially because identification of Mesembryanthema (Aizoaceae), the second largest family in the biome, is notoriously difficult (Smith et al. 1998). No attempts have been made, as yet, to estimate the degree of error in this data set.

Using survey data from a variety of projects that used different relevé sizes is not a significant source of error. Varying the relevé area by an order of magnitude either way (i.e., 10 to 1000 m²) changed the z-value by less than 0.01%. Therefore, knowing the size of the sample relevé does not underpin the application of this technique. Consequently, variable survey area size is not a constraint to using this method. As long as the sample areas are within an order of magnitude of each other, they can be combined for the purposes of estimating targets.

These problems highlight the great need for systematic data collection over a variety of scales, to allow for proper comparisons of z-values at local, regional, and global scales. It is imperative that all of this is done in a highly standardized manner, and having in mind comparisons at the scale considered. Once such data would be available, they would constitute a great starting point for systematic and biologically meaningful target setting.

Another source of error lies in the delimitation of land-class boundaries. The vegetation types used here were mapped using expert knowledge. Errors in where the “true” boundaries of the vegetation types lie can lead to over- or underestimation of z-values. For example, the boundaries of the Eastern Bushmanland Quartz and Gravel Patch vegetation type, as used in this study, are incorrect. In revised versions of the South African vegetation map, this vegetation type has been divided between three vegetation types (one new and two existing; L. Mucina, personal communication). The resultant vegetation map not only agrees better with expert assessment, but also the vegetation types are more homogeneous and better reflect landscape-level vegetation patterns. The consequences for the targets are that they will have to be revisited for this area, and relevés will have to be reassigned to vegetation types according to the new boundaries. The calculated target cannot be extrapolated from the old vegetation type to the new ones. Another problem that arises as a result of incorrect vegetation-type boundaries is that relevés are incorrectly assigned to a vegetation type. Realistically, such errors can be controlled only through wide expert involvement in the delimitation of land-class boundaries, whether using expert mapping or modeling techniques.

Extrapolating z-values

Within a biogeographic province (i.e., vegetation-type group) there is considerable variation in z-values. There is, however, a generally accepted strong relationship between species diversity and habitat diversity (Holland 1978, Miller et al. 1995, Rosenzweig 1995), which was confirmed in this study. Using topographic diversity as a surrogate for habitat diversity, we constructed a model that relates z-values to an independent land-class metric that can be generated from remotely derived GIS data. The advantages of taking this step are substantial. It is now possible to approximate a z-value for all land classes in the Succulent Karoo, based on a measure of the diversity of habitats. Geographic location is important in explaining the pattern in z-values. This may reflect the historical influence of dynamic environments on the evolution of regional floras in and away from local centers of diversity or refugia.

For the Succulent Karoo vegetation types, where there are not enough vegetation types in a category to build a significant model incorporating topographic diversity, the equally strong observed relationships between z-values and geographic location support the approach of assigning z-values to vegetation types in the same group, using the nearest neighbor principle. This approach would hold at least within vegetation groups within a biome.

It is difficult to make predictions for other biomes. It is almost certain that other biomes will have a range in z-values and, hence, targets. This study makes it very clear that no single target will be suitable for all land classes within a region. As a very general rule, land classes with large numbers of range-restricted species will have higher targets. Whether there is a relationship between endemicity or rarity and z-values will need to be determined before more empirical statements can be made. Also, more topographically diverse land classes will have relatively higher z-values.

General

The idea of using the SAR for setting conservation targets has been around for some time (May 1975, Diamond and May 1976, Rosenzweig 1995, Vreugdenhil et al. 2003). This work, however, represents the first attempt to quantitatively determine conservation targets for land classes using the SAR based on actual biodiversity data. Exciting as this advance is, the limitations of this approach, in terms of input data requirements, data error, and model assumptions, must not be forgotten.

Conservation practitioners also need to bear in mind that applying SAR targets is only one of many types of conservation targets. This target is based on the hypothesized accumulation of species in a sample of conservation areas. It does not explicitly take into account multiple occurrences of species, nor does it tell us anything about where, within a land class, the target should be achieved to conserve the target percentage of species. Also, these targets do not tell us anything about requirements for ecological processes. It is important to remember that the SAR target does not replace other approaches to setting targets that focus, for example, on minimum viable populations, meta-population dynamics, or ecological processes.

From a practical perspective, the two major limitations of binary or fixed conservation targets need to be stressed. Firstly, fixed targets distort the effectiveness of conservation implementation. Using fixed targets, it is possible to achieve targets for land classes that are just below target, and that probably require minimal effort to achieve, while ignoring those land classes that are far below target and that require significantly more effort to achieve their targets. This approach of picking the low-hanging fruits, although not always the case, exaggerates the success of conservation implementation while exposing the most vulnerable components, i.e., those least conserved, to potentially greater risk through being sidelined by the implementation process.

Secondly, fixed targets promote the land-use philosophy of “clearing down to target.” This is a dangerous philosophy, as it is generally accepted that one requires more than just each species represented in a reserve to conserve biodiversity. The SAR target approach applied here does not take into account ecological processes.

Survey plots are little more than slightly-less-than-random-samples of the complete biodiversity present at any point in space. These data, however, have formed the basis of much of the ecological research into how terrestrial systems are structured and work. It is important to make the best use of available information rather than wait for better data. Biologically informed decisions need to be made regarding conservation action and landscape management. The methodology for setting conservation targets presented here is by no means a “save-all” solution to the problem of setting targets. It should be viewed as a tool that complements, rather than replaces, existing empirical or expert-based species, population, habitat, or ecosystem targets. This method is fraught with methodological and data assumptions that need to be addressed, but in the meantime, it would be wise to apply the method, being mindful of its limitations, rather than wait until these problems have been resolved.

It must reiterated that this work makes it clear that the IUCN 10% target is inadequate for capturing the majority of plant diversity within the Succulent Karoo Biome. This trend is probably true for many other terrestrial ecosystems. Further, land classes are not all equal from a biodiversity perspective, and setting a single target for all land classes does not make good conservation sense.

Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.

Simon Ferrier, Dan Faith, Janet Franklin, Frank Davis, William Bond, and the reviewer are thanked for their insightful and constructive contributions to the development of this paper. We are grateful to the Critical Ecosystem, Partnership Fund for funding via the Succulent Karoo Ecosystem Planning Project and to the Global Environment Facility for funding via the Subtropical Ecosystem Planning Project.

The summary of model parameters relating z-values to independent landscape variables for the three Succulent Karoo vegetation groups presented in Figs. 3, 4, 5, and 6.

Acosta, C. A., and D. N. Robertson. 2002. Diversity in coral reef fish communities: the effects of habitat patchiness revisited. Marine Ecology-Progress Series 227:87–96.

Armesto, J. J., R. Rozzi, C. Smith-Ramirez, and M. T. K. Arroyo. 1998. Ecology - Conservation targets in South American temperate forests. Science 282(5392): 1271–1272.

Barnard, P., C. J. Brown, A. M. Jarvis, R. Robertson, and L. van Rooyen. 1998. Extending the Namibian protected area network to safeguard hotspots of endemism and diversity. Biodiversity and Conservation 7(4):531–547.

Bedward, M., D. A. Keith, and R. L. Pressey. 1992. Homogeneity analysis - Assessing the utility of classifications and maps of natural-resources. Australian Journal of Ecology 17:133–139.

Bond, W., J. Midgley, and J. Vlok. 1988. When is an island not an island? Insular effects and their causes in fynbos shrublands. Oecologia 77:515–521.

Bond, W. J. 1993. Keystone species. Pages 237–253 in E. D. Schultze and H. A. Mooney, editors. Biodiversity and ecosystem function. Springer-Verlag, Berlin, Germany.

Boshoff, A., and G. Kerley. 1999. Conservation planning in the Cape Floristic Region: distribution, conservation status and spatial population requirements of the medium- to large-sized mammals. Terrestrial Ecology Research Unit, University of Port Elizabeth, Port Elizabeth, South Africa.

Boshoff, A., G. Kerley, and R. Cowling. 2001. A pragmatic approach to estimating the distributions and spatial requirements of the medium- to large-sized mammals in the Cape Floristic Region, South Africa. Diversity and Distributions 7:29–43.

Brooks, T. M., S. L. Pimm, and J. O. Oyugi. 1999. Time lag between deforestation and bird extinction in tropical forest fragments. Conservation Biology 13:1140–1150.

Brose, U. 2002. Estimating species richness of pitfall catches by non-parametric estimators. Pedobiologia 46:101–107.

Brown, M., and J. J. Dinsmore. 1988. Habitat islands and the equilibrium theory of island biogeography - Testing some predictions. Oecologia 75(3):426–429.

Burgman, M. A., H. P. Possingham, A. J. J. Lynch, D. A. Keith, M. A. McCarthy, S. D. Hopper, W. L. Drury, J. A. Passioura, and R. J. Devries. 2001. A method for setting the size of plant conservation target areas. Conservation Biology 15(3):603–616.

Calkin, D. E., C. A. Montgomery, N. H. Schumaker, S. Polasky, J. L. Arthur, and D. J. Nalle. 2002. Developing a production possibility set of wildlife species persistence and timber harvest value. Canadian Journal of Forest Research-Revue Canadienne De Recherche Forestiere 32(8):1329–1342.

Chiarucci, A., N. J. Enright, G. L. W. Perry, B. P. Miller, and B. B. Lamont, B. 2003. Performance of nonparametric species richness estimators in a high diversity plant community. Diversity and Distributions 9:283–295.

Collins, M. D., D. P. Vazquez, and N. J. Sanders. 2002. Species–area curves, homogenization and the loss of global diversity. Evolutionary Ecology Research 4:457–464.

Colwell, R. 1997. EstimateS: Statistical estimation of species richness and shared species from samples. Version 5. User's guide and application published online. [URL: a href="http://viceroy.eeb.uconn.edu/estimates"http://viceroy.eeb.uconn.edu/estimates]

Colwell, R., and J. Coddington. 1995. Estimating terrestrial biodiversity through extrapolation. Pages 101–118 in D. Hawksworth, editor. Biodiversity: measurement and estimation. The Royal Society and Chapman and Hall, London, UK.

Cornelius, C., H. Cofre, and P. A. Marquet. 2000. Effects of habitat fragmentation on bird species in a relict temperate forest in semiarid Chile. Conservation Biology 14:534–543.

Cowling, R., and W. Bond. 1991. How small can reserves be? An empirical approach in Cape Fynbos, South Africa. Biological Conservation 58:243–256.

Cowling, R., R. Pressey, A. Lombard, P. Desmet, and A. Ellis. 1999a. From representation to persistence: requirements for a sustainable reserve system in the species-rich mediterranean-climate deserts of southern Africa. Diversity and Distributions 5:51–71.

Cowling, R. M., K. J. Esler, and P. W. Rundel. 1999b. Namaqualand, South Africa - an overview of a unique winter-rainfall desert ecosystem. Plant Ecology 142(1-2):3–21.

Cowling, R. M., and R. L. Pressey. 2001. Rapid plant diversification: planning for an evolutionary future. Proceedings of the National Academy of Sciences (USA) 98(10):5452–5457.

Darlington, P. 1957. Zoogeography. John Wiley, New York, New York, USA.

Dean, W., and S. Milton, editors. 1999. The Karoo: ecological patterns and processes. Cambridge University Press, Cambridge, UK.

Debinski, D. M., and R. D. Holt. 2000. A survey and overview of habitat fragmentation experiments. Conservation Biology 14:342–355.

Deshaye, J., and P. Morisse 1989. Species-area relationships and the SLOSS effect in a Subarctic Archipelago. Biological Conservation 48:265–.

Diamond, J., and R. May. 1976. Island biogeography and the design of natural reserves. Pages 163–186 in R. May, editor. Theoretical ecology: principles and applications. Blackwell Scientific Publications, Oxford, UK.

Driver, A., P. G. Desmet, M. Rouget, R. M. Cowling, and K. E. Maze. 2003. Succulent Karoo Ecosystem Plan Biodiversity Component Technical Report. Cape Conservation Unit, Botanical Society of South Africa, Cape Town, South Africa.

Faith, D. P. 2003. Environmental diversity (ED) as surrogate information for species-level biodiversity. Ecography 26(3):374–379.

Ferguson, M. E., B. V. Ford-Lloyd, L. D. Robertson, N. Maxted, and H. J. Newbury. 1998. Mapping the geographical distribution of genetic variation in the genus Lens for the enhanced conservation of plant genetic diversity. Molecular Ecology 7:1743–1755.

Ferrier, S. 2002. Mapping spatial pattern in biodiversity for regional conservation planning: where to from here? Systematic Biology 51:331–363.

Ferrier, S., M. Drielsma, G. Manion, and G. Watson. 2002. Extended statistical approaches to modelling spatial pattern in biodiversity in northeast New South Wales. II. Community-level modelling. Biodiversity and Conservation 11:2309–2338.

Fleisman, E., D. D. Murphy, and P. F. Brussard. 2000. A new method for selection of umbrella species for conservation planning. Ecological Applications 10:569–579.

Gonzalez, A. 2000. Community relaxation in fragmented landscapes: the relation between species richness, area and age. Ecology Letters 3:441–448.

Gould, S. J. 1979. An allometric interpretation of species-area curves: the meaning of the coefficient. American Naturalist 114:335–343.

Haila, Y. 2002. A conceptual genealogy of fragmentation research: from island biogeography to landscape ecology. Ecological Applications 12:321–334.

Harte, J., A. Kinzig, and J. Green. 1999a. Self-Similarity in the distribution and abundance of species. Science 284:334–336.

Harte, J., S. McCarthy, K. Taylor, A. Kinzig, and M. L. Fischer, M. L. 1999b. Estimating species–area relationships from plot to landscape scale using species spatial-turnover data. Oikos 86:45–54.

Herzog, S. K., M. Kessler, and T. M. Cahill. 2002. Estimating species richness of tropical bird communities from rapid assessment data. Auk 119:749–769.

Holland, P. G. 1978. An evolutionary biogeography of the genus Aloe. Journal of Biogeography 5:213–226.

Kelt, D. A. 2001. Differential effects of habitat fragmentation on birds and mammals in Valdivian temperate rainforests. Revista Chilena De Historia Natural 74:769–777.

Kemper, J., R. Cowling, and D. Richardson. 1999. Fragmentation of South African renosterveld shrublands: effects on plant community structure and conservation implications. Biological Conservation 90:103–111.

Kinzig, A., and J. Harte. 2000. Implications of endemics–area relationships for estimates of species extinctions. Ecology 81:3305–3311.

Kirkpatrick, J. B., and M. J. Brown. 1994. A comparison of direct and environmental domain approaches to planning reservation of forest higher-plant communities and species in Tasmania. Conservation Biology 8:217–224.

Knowles, L. L. 2001. An evolutionary slant on species–area curves. Trends in Ecology and Evolution 16:174–175.

Lacy, R. 1997. Importance of genetic variation to the viability of mammalian populations. Journal of Mammalogy 78:320–335.

Lambeck, R. J. 1997. Focal species: a multi-species umbrella for nature conservation. Conservation Biology 11:849–857.

Launer, A. E., and D. D. Murphy. 1994. Umbrella species and the conservation of habitat fragments: a case study of a threatened butterfly and a vanishing grassland ecosystem. Biological Conservation 69:145–153.

Lawton, J. H. 1988. More time means more variation. Nature 334(18):563.

Lindenmayer, D. B., and R. C. Lacy. 1995. Metapopulation viability of Leadbeater possum, Gymnobelideus leadbeateri, in fragmented old-growth forests. Ecological Applications 5:164–182.

Lombard, A. T., R. M. Cowling, R. L. Pressey, and A. G. Rebelo. 2003. Effectiveness of land classes as surrogates for species in conservation planning for the Cape Floristic Region. Biological Conservation 112(1-2):45–62.

Lomolino, M. V. 2000. Ecology's most general, yet protean pattern: the species–area relationship. Journal of Biogeography 27(1):17–26.

Lomolino, M. V. 2001. The species–area relationship: new challenges for an old pattern. Progress in Physica Geography 25:1–21.

Lomolino, M. V. 2002. The species–area relationship does not have an asymptote - Comment. Journal of Biogeography 29:555–557.

Lomolino, M. V., and D. R. Perault. 2001. Island biogeography and landscape ecology of mammals inhabiting fragmented, temperate rain forests. Global Ecology and Biogeography 10:113–132.

Lomolino, M. V., and M. D. Weiser. 2001. Towards a more general species–area relationship: diversity on all islands, great and small. Journal of Biogeography 28:431–445.

Magura, T., V. Kodobocz,and B. Tothmeresz. 2001. Effects of habitat fragmentation on carabids in forest patches. Journal of Biogeography 28:129–138.

Margules, C., and R. Pressey. 2000. Systematic conservation planning. Nature 405:243–253.

Margules, C. R., A. O. Nicholls, and R. L. Pressey. 1988. Selecting networks of reserves to maximise biological diversity. Biological Conservation 43:63–6.

May, R. 1975. Patterns of species abundance and diversity. Pages 81–120 in M. Cody and J. Diamond, editors. Ecology and evolution of communities. Belknap Press of Harvard University, Cambridge, Massachusetts, USA.

Miller, J. R., and P. Cale. 2000. Behavioral mechanisms and habitat use by birds in a fragmented agricultural landscape. Ecological Applications 10:1732–1748.

Miller, R. E., J. M. Ver Hoef, and N. L. Fowler. 1995. Spatial heterogeneity in eight central Texas grasslands. Journal of Ecology 83:919–928.

Mills, L. S., M. E. Soulé, and D. F. Doak. 1993. The keystone species concept in ecology and conservation. BioScience 43(4):219–224.

Mittermeier, R. A., N. Myers, J. B. Thomsen, G. A. B. da Fonseca, and S. Olivieri. 1998. Biodiversity hotspots and major tropical wilderness areas: approaches to setting conservation priorities. Conservation Biology 12:516–520.

Noss, R. 1996. Protected areas: how much is enough? Pages 91–120 in R. Wright, editor. National parks and protected areas. Blackwell, Cambridge, UK.

Noss, R., J. Strittholt, K. Vance-Borland, C. Carroll, and P. Frost. 1999. Conservation plan for the Klamath-Siskiyou ecoregion. Natural Areas Journal 19(4):392–411.

Nunney, L., and K. A. Campbell. 1993. Assessing minimum viable population size: demography meets population genetics. Trends in Ecology and Evolution 8:234–239.

Petersen, F. T., R. Meier, and M. Nykjaer. 2003. Testing species richness estimation methods using museum label data on the Danish Asilidae. Biodiversity and Conservation 12:687–701.

Pressey, R. L., R. M. Cowling, and M. Rouget. 2003. Formulating conservation targets for biodiversity pattern and process in the Cape Floristic Region, South Africa. Biological Conservation 112(1-2):99–127.

Pressey, R. L., T. C. Hager, K. M. Ryan, J. Schwarz, S. Wall, S. Ferrier, and P. M. Creaser. 2000. Using abiotic data for conservation assessments over extensive regions: quantitative methods applied across New South Wales, Australia. Biological Conservation 96:55–82.

Preston, F. 1948. The commonness, and rarity, of species. Ecology 29:254–83.

Prins, A. H., G. A. Dijkstra, and R. M. Bekker. 1998. Feasibility of target communities in a Dutch brook valley system. Acta Botanica Neerlandica 47(1):71–88.

Robinson, W. D. 1999. Long-term changes in the avifauna of Barro Colorado Island, Panama, a tropical forest isolate. Conservation Biology 13(1):85–97.

Rodrigues, A. S. L., and K. J. Gaston. 2001. How large do reserve networks need to be? Ecology Letters 4(6):602–609.

Rosenzweig, M. 1995. Species diversity in space and time. Cambridge University Press, Cambridge, UK.

Rouget, M., D. M. Richardson, R. M., Cowling, J. W. Lloyd, and A. T. Lombard. 2003. Current patterns of habitat transformation and future threats to biodiversity in terrestrial ecosystems of the Cape Floristic Region, South Africa. Biological Conservation 112(1-2):63–85.

Saetersdal, M., J. M. Line, and H. J. B. Birks. 1993. How to maximise biological diversity in nature reserve selection: vascular plants and breeding birds in deciduous woodlands of western Norway. Biological Conservation 66:131–138.

Sanderson, E., K. Redford, A. Vedder, P. Coppolillo, and S. Ward. 2002. A conceptual model for conservation planning based on landscape species requirements. Landscape and Urban Planning 58:41–46.

Schmiedel, U. 2002. Quartz fields of southern Africa: flora, phytogeography, vegetation, and habitat ecology. Dissertation. University of Cologne, Colgne, Germany.

Schmiedel, U., and N. Jürgens. 1999. Community structure on unusual habitat islands: quartz-fields in the Succulent Karoo, South Africa. Plant Ecology 142(1–2):57–69.

Scott, J. M., F. W. Davis, R. G. McGhie, R. G. Wright, C. Groves, and J. Estes. 2001. Nature reserves: Do they capture the full range of America's biological diversity? Ecological Applications 11:999–1007.

Seabloom, E. W., A. P. Dobson, and D. M. Stoms. 2002. Extinction rates under non-random patterns of habitat loss. Proceedings of the National Academy of Sciences (USA) 99:11229–11234.

Smith, G., P. Chesselet, E. van Jaarsveld, H. Hartmann, S. Hammer, B.-E. van Wyk, P. Burgoyne, C. Klak, and H. Kurzweil. 1998. Mesembs of the world. Briza Publication, Pretoria, South Africa.

Soulé, M. E., and M. A. Sanjayan. 1998. Ecology - Conservation targets: Do they help? Science 279:2060–2061.

Tilman, D., R. May, C. Lehman, and M. Nowak. 1994. Habitat destruction and the extinction debt. Nature 371:65–66.

Travaini, A., M. Delibes, P. Ferreras, and F. Palomares. 1997. Diversity, abundance or rare species as a target for the conservation of mammalian carnivores: a case study in Southern Spain. Biodiversity and Conservation 6:529–535.

Tscharntke, T., I. Steffan-Dewenter, A. Kruess, and C. Thies. 2002. Characteristics of insect populations on habitat fragments: a mini review. Ecological Research 17(2):229–239.

Turner, A., C. Rubec, and E. Wiken. 1992. Canadian ecosystems: a systems approach to their conservation. Pages 117–127 in J. H. M. Willison, S. Bondrup-Nielsen, C. Drysdale, T. B. Herman, N. W. P. Munro, and T. L. Pollock, editors. Science and the management of protected areas. Elsevier, Amsterdam, The Netherlands.

Turner, A. M., J. C. Trexler, C. F. Jordan, S. J. Slack, P. Geddes, J. H. Chick, and W. F. Loftus. 1999. Targeting ecosystem features for conservation: standing crops in the Florida Everglades. Conservation Biology 13:898–911.

Turnipseed, M., K. E. Knick, R. N. Lipcius, J. Dreyer, and C. L. Van Dover. 2003. Diversity in mussel beds at deep-sea hydrothermal vents and cold seeps. Ecology Letters 6:518–523.

Vreugdenhil, D., J. Terborgh, A. Cleef, M. Sinitsyn, M. Boere, M., V. Archaga, and H. Prins. 2003. Comprehensive protected areas system composition and monitoring. WICE (World Institute for Conservation and Environment), Shepherdstown, West Virginia, USA.

Wright, S. J. 1988. Patterns of abundance and the form of the species–area relation. American Naturalist 131:401–411.

Zurlini, G., L. Grossi, and O. Rossi. 2002. Spatial-accumulation pattern and extinction rates of Mediterranean flora as related to species confinement to habitats in preserves and larger areas. Conservation Biology 16:948–963.