|
|
|
Copyright ©1999 by The Resilience Alliance*
The following is the established format for referencing this article:
Janssen, M. A. and S. R. Carpenter. 1999. Managing the Resilience of Lakes: A multi-agent modeling approach. Conservation Ecology 3(2): 15. [online] URL: http://www.consecol.org/vol3/iss2/art15/
A version of this article in which text, figures, tables, and appendices are separate files may be found by following this link.
Research, part of Special Feature on Recent Advances in Ecological Theory and Practice Managing the Resilience of Lakes: A Multi-agent Modeling Approach Marco A. Janssen1 and Stephen R. Carpenter2
1Free University; 2University of Wisconsin
- Abstract
- Introduction
- Myths of Nature, Cultural Types, and Resilience of Systems
- Lake Eutrophication
- A Simple Lake Model
- Including a Slow Variable: the Mud
- Changing Perspectives and Adaptive Responses
- Conclusions
- Responses to this Article
- Acknowledgments
- Literature Cited
- Appendix 1
We demonstrate an approach for integrating social and ecological models to study ecosystem management strategies. We focus on the management of lake eutrophication. A model has been developed in which the dynamics of the lake, the learning dynamics of society, and the interactions between ecology and society are included. Analyses with the model show that active learning is important to retain the resilience of lakes. Although very low levels of phosphorus in the water will not be reached, active learning reduce the chance of catastrophic high phosphorus levels.
KEY WORDS: active learning, eutrophication, integrated modeling, lake dynamics, lake management, multi-agent modeling, phosphorus, resilience, restoration, simulation.
Published: November 24, 1999
Human social dynamics are of vital importance to understanding degradation, restoration, and sustainability of our environment. For example, destructive management of ecosystems can often be related to social institutional frameworks, although our understanding of these relations is rather limited (Blaikie and Brookfield 1987). Because our understanding of social dynamics is rather fragmented in many issues, focusing on any one type of model of social dynamics in relation to ecosystem management limits our insights. This is the reason why the Resilience Network, an international network of ecologists and economists, has developed a series of simple models for the management of lake eutrophication. Other studies have used stochastic optimization (Carpenter et al. 1999a), agent-based models of market and political interactions (Carpenter et al. 1999b), and interactive simulation games (Carpenter et al. 1999b).
In this paper, we apply a multi-agent approach, in line with Janssen and de Vries (1998), to describe a model in which the dynamics of the lake, the learning dynamics of society, and the interactions between ecology and society are included. These exercises should give us more insight into possible consequences of ecosystem management and provide us with a toolbox of approaches to be applied in real-life case studies. We assume that lake managers do not precisely know the dynamics of the lake. Each agent assumes a certain "myth of nature," which they use to determine how they will manage the lake. The dynamics of the lake, however, may change in response to management or natural surprises.
The paper is organized as follows. First, we will discuss some methodological issues about resilience of systems, myths of nature, and cultural types. Next, we will give a brief overview of the problem of lake eutrophication. In the fourth section, a simple lake model is introduced in which we will assess the consequences if society acts according to a valid or invalid myth of nature. In the fifth section, we add an additional slow variable to the model and assume that agents are not aware of the dynamics. Then we assume that society may learn if confronted with surprised dynamics of the lake. Finally, we will conclude with some lessons for the management of ecosystems. In the Appendix, we have included a demo-version of the model; readers are encouraged to experiment with it.
Perspectives or worldviews, to an important extent, determine the attitudes toward society and the environment evolved during history. These have been classified in various ways. One of these classifications is the Cultural Theory of Thompson et al. (1990), which aims to give a general description of natural and human systems and social relations. Because the Cultural Theory provides us with a rather deterministic description of agents with different rationalities, we are able to apply it within an integrated simulation model. Detailed descriptions of the Cultural Theory and applications in multi-agent modeling can be found in Schwartz and Thompson (1990), Thompson et al. (1990), Price and Thompson (1997), Janssen (1998), and Janssen and de Vries (1998). Thompson et al. (1990) claim that heterogeneity among worldviews can be classified by five perspectives: hierarchist, egalitarian, fatalist, individualist, and hermit. The adoption of perspectives is a dynamic process. Change occurs because of "surprise," that is, the discrepancy between the expected and the actual, which is of central importance in dislodging individuals from a previously adopted perspective. Following Rayner (1991), the "active" perspectives, those of the hierarchist, the egalitarian, and the individualist, are taken into account, so that the autonomous and the fatalist perspectives are disregarded. The hermit, as an exponent of the autonomous perspective, is not interested in what happens in the world, but prefers to distance himself from it. The fatalist, for whom everything is a lottery (behavior of both humans and nature being unpredictable), is likewise not examined. Exclusion of the fatalist and the hermit might be not satisfactory. However, our purpose is not to model the Cultural Theory, but to include important insights from it into an integrated framework. By translating concepts into mathematical formats, we unfortunately lose some nuance. The main purpose is the acknowledgement of different perspectives. The egalitarian, hierachist, and individualist can be assumed to be extremes of a continuum of perspectives (Rayner 1991).
The three "active" perspectives from Cultural Theory (hierarchist, egalitarian, and Individualist) can be viewed as the corners of a triangle.
- Hierarchists believe that humans are born sinful, but can nevertheless be redeemed by virtuous institutions. Nature is stable in most circumstances, but can collapse if it crosses the limits of capacity. Therefore, control is advocated as management style.
- Egalitarians believe that human beings are born virtuous but are also highly malleable by evil institutions. Nature is highly unstable, and the least human intervention may lead to complete collapse. A management style that prevents heavy intrusion by humans is preferred.
- Individualists believe that humans are self-seeking and unmalleable. Nature provides an abundance of resources and is believed to remain stable under human interventions. A reactive management style is advocated.
Of course, in the real world, actors rarely express their views in such an exaggerated way. They are in constant interaction and often have strategic and public relations in mind as well. Moreover, positions may be non-identical or even inconsistent when stakeholders share only part of the underlying values and judgments. Nevertheless, this framework captures the crucial idea that a set of heterogeneous agents can share a worldview and preferred management style (Janssen and de Vries 1998).
When an agent's worldview matches the real dynamics of the system, the agent's corresponding management style leads to a utopia (Fig. 1). In contrast, the dystopias describe what would happen to the world if an agent's favored strategy were to be applied while reality seemed to follow another worldview. Comparison of utopias gives us an idea of different possible preferred states of the system, preferred under different perspectives. Dystopias give us an idea of the expected risk of having a wrong idea about the dynamics of the system, i.e., being too risk- aversive or too risk-taking according to the utopian case. In fact, the occurrences of dystopias are surprises that may lead to changing perspectives of the agents. In this paper, we simulate such changes.
Fig. 1. Combinations of management style and worldview lead to utopias and dystopias.

|
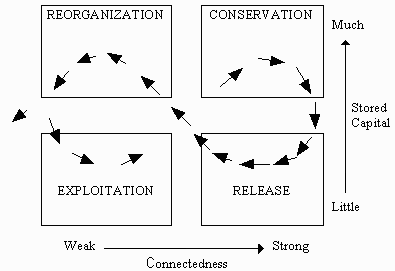
An interesting framework to explain the transitions in behavior of the system is the approach of Holling (1986), who proposes four basic functions common to all complex systems, and a spiralling evolutionary path through them (Fig. 2). This evolutionary cycle can be used to explain transitions in social systems, as well as in ecosystems (Holling et al., in press). The central idea is that the four-phase adaptive cycle emphasizes a loop from conservation to two phases of destruction and reorganization in which innovation and chance assume dominant roles. The reorganization phase occurs when a rare and unexpected intervention or event can shape a new future. Holling et al. (in press) argue that in this stage, when the system is in a state most likely to be transformed by innovation, agents have the greatest potential to influence the future of the system. Note that the system can also exit the cycle and flip into a new kind of system.
The patterns produced by these four phases are discontinuous and dependent on the interaction of processes that trigger and organize the release and reorganization functions. These interactions create multiple stable states. An illustrative example is the budworm outbreak (Holling 1978). Successful suppression of spruce budworm populations in eastern Canada, using insecticides, certainly preserved the pulp and paper industry and employment in the short term by partially protecting the forest. However, this policy has left the forest and the economy more vulnerable to an outbreak over a larger area and of an intensity not experienced before. More recent examples include livestock problems in Western Europe, "mad cow disease," the pig plague, and poisonous chickens. In these examples, local human influences slowly accumulate to trigger sudden, abrupt changes that may effect the vitality of societies. There are counteractive forces that give ecological systems the resilience and adaptability to deal with considerable change, and that provide people with the capacity to innovate and create (Holling 1994). However, nature, people, and economies are suddenly now co-evolving on a planetary scale, each affecting the others in such novel ways and on such a large scale that large surprises may overwhelm the adaptive and innovative capabilities of people (Holling 1994). The question of sustainable development is, therefore, how to stimulate a sustainable co-evolution of human activities and environmental change.
Lakes are often classified as oligotrophic (leading to clear water and high value to society) or eutrophic (leading to poor water quality and low value to society) depending on their productivity (Odum 1997, Wilson and Carpenter 1999). Eutrophication, caused by excess of inputs of nutrients, is a widespread and growing problem of lakes, rivers, estuaries, and coastal oceans (Smith 1998). In lakes, excessive inputs of phosphorus (P) are usually the primary cause (Schindler 1977). Negative effects of eutrophication include increased plant growth; shifts in phytoplankton to bloom-forming species that are often toxic or inedible; decreases in water transparency; problems with taste, odor, and water treatment; oxygen depletion; and fish kills (Smith 1998). Thus, a nutrient-poor lake is preferable to a fertile one from the standpoint of water use and recreation (Wilson and Carpenter 1999). Most of the excess phosphorus input to waters in developed nations is caused by nonpoint pollution as runoff from agriculture and urban lands (Carpenter et al. 1998). Because sources are diffuse, this pollution is difficult to measure and regulate. Ironically, due to intense efforts to increase the fertility of the land, waters have problems of excess fertility that impair water supply and create the need for costly remediations.
Although nutrient addition may lead to immediate increases in symptoms of eutrophication, decreased nutrient input does not always cause immediate or complete reversal of eutrophication (Sas 1989, Cooke et al. 1993). Explanations for delayed response, or lack of response, by lakes to reduced nutrient input focus on recycling of phosphorus. As lakes are enriched, P accumulates in sediments, and rates of recycling from sediments to the overlying water ("internal loading") increase. Whole-lake experiments show that recycling rates can build to significant levels in a matter of years (Schindler et al. 1987). Lakes with human-induced eutrophication may receive excessive P inputs for decades or longer. On an annual basis, recycling from sediments in eutrophic lakes commonly exceeds inputs of P (Nurnberg 1984, Soranno et al. 1997). Recycling of P from sediments interferes with mitigation of eutrophication, and can sustain eutrophy long after external inputs of P are decreased (Sas 1989, Cooke et al. 1993). In some cases, eutrophication cannot be reversed by decreasing P input alone (Larson et al. 1979, 1981, Cooke et al. 1993, Scheffer et al. 1993). Such lakes need additional interventions that decrease recycling, accelerate sedimentation, or increase outputs of P.
The essential dynamics of lake eutrophication can be described by the following equation (Carpenter et al. 1999b):
P[t] = (1-b) P[t-1] + L[t] + r*P[t-1]q / (mq + P[t-1]q)
where P is the amount of phosphorus (mass or concentration) in the water; L is the annual phosphorus input from human activities (mass or concentration per unit time); and b is the proportion of P lost at each time step. The maximum recycling rate of phosphorus (mass or concentration per unit time) is r. We will assume that sediments are the major source of recycled phosphorus (ignoring the recycling by consumers). The overall recycling rate is assumed to be a sigmoid function of P. The exponent q (>=2) affects the steepness of the sigmoid curve. Empirical limnological models provide a rough estimate of q ranging from approximately 20 for shallow, warm lakes to approximately 2 for deep, cold lakes. The value of P at which recycling reaches half of the maximum rate is m.
The lake has alternative states of oligotrophy or eutrophy for certain values of the parameters (Carpenter et al. 1999a). Oligotropic lakes are characterized by low nutrient inputs, low- to-moderate levels of plant production, relatively clear water, and relatively high economic value of ecosystem services. Eutrophic lakes have high nutrient inputs, high plant production, murky water with problems including anoxia and toxicity, and relatively low value of ecosystem services. Note that when eutrophication is being mitigated, lakes can respond differently to reduced P inputs. Three types of lakes can be distinguished (Carpenter et al. 1999a).
Reversible lakes: eutrophication can be reversed by P input controls alone.
Hysteretic lakes: eutrophication can be reversed by severely reducing P inputs for an extended period of time, or by combining P input controls with temporary interventions such as chemical treatment.
Irreversible lakes: eutrophication cannot be reversed even by severe reductions in P input, although it may be reversed in some cases by additional costly interventions.
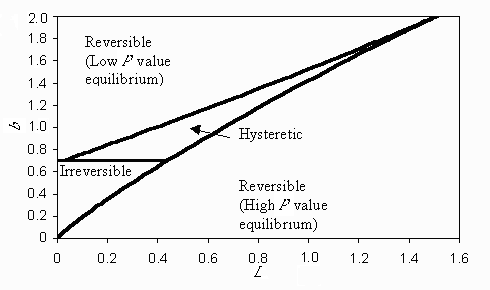
One can derive a bifurcation diagram (Fig. 3) in which the different types of lakes are viewed as a function of parameters of the lake model. Carpenter et al. (1999a) define a reversible lake as having one stable point (we will only look at a reversible lake of low P-value stable points), and hysteretic and irreversible lakes are defined as lakes having three equilibria, of which two are stable (a low-P steady state and a high-P steady state) and one is unstable. The line separating the reversible lakes from the hysteretic and irreversible lakes depicts the parameter values for which there are exactly two equilibria that are both stable. The difference between hysteretic and irreversible lakes is the possibility of shifting from the high-P steady state to the low-P steady state. In the case of an irreversible lake, inputs should become negative to derive such a shift, which is, by definition, impossible. For mathematical details of this bifurcation diagram, we refer to Carpenter et al. (1999a).
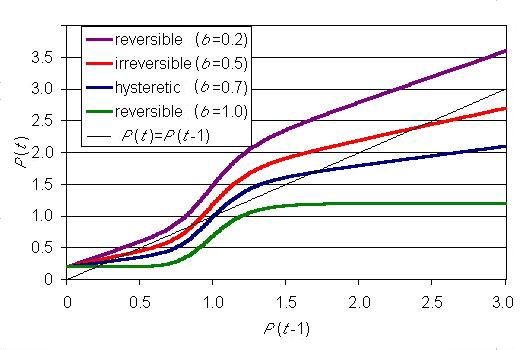
Dynamics of the different types of lakes are visualized in Fig. 4. Given a constant input value (L = 0.2), the relation between P[t] and P[t-1] for different values of b are given. At a very low level of b, the lake has one equilibrium, although this is one with a high value of P. As b increases, the lake has three equilibria (an intersection with a diagonal line (P[t] = P[t-1])), of which the middle one is not stable. At a high value of b, the lake has one equilibrium again, but now with a low value of P
Fig. 4. Dynamic of the simple lake model for different assumption of b, the proportionate loss of P at each time step.
|
These different dynamics of the lake correspond with the different myths of nature. The individualistic perspective (Nature is benign) relates to the reversible lakes (with the low-P steady state) in which eutrophication can be reversed if necessary. The hierarchist perspective (Nature is perverse/tolerant) comes close to describing the hysteretic lakes in which careful (scientific) management is needed to control the eutrophication. The egalitarian perspective (Nature is ephemeral or fragile) relates to irreversible lakes that require precautionary measures to limit nutrient inputs. For the egalitarian perspective, a low value of b is assumed (b = 0.3), in contrast to the individualistic perspective (b = 1.5). For the hierarchistic perspective, we assume a hysteretic lake (b = 0.8).
The input of phosphorus into the lake is the result of a cost/benefit analysis. The utility of activities that result in phosphorus inputs is directly related to the input: Ua[t] = a*L[t]. The utility of the water quality is related to the concentration of phosphorus in the water. Following Carpenter et al. (1999a), we assume that Uw[t] = β0-β1 (P[t] /m)2. The cost-benefit problem can therefore be described as
Max SUM(t = 0 to tmax, Δt * (a*L[t] + (β0 - β1 (P[t] /m)2)
L
s.t.P[t] = (1-b)P[t-1] + L[t] +P[t-1]q/(mq+P[t-1]q)
where "s.t." means subjected to; L is the decision variable for the maximization problem.
As discussed in the section Myths of nature, cultural types, and resilience of systems, different types of management styles can be distinguished. An egalitarian management style is simulated by using a low discount rate (Δ= 0.99) and a high value of the quality of water (β1 = 0.9). The individualists are more focused on short-term returns and therefore use a high discount rate (Δ= 0.9). Furthermore, the individualists value the quality of water less than do the egalitarians (β1=0.7). The hierarchists' management style is simulated by parameter values in between those of the egalitarian and the individualist (Δ= 0.96, β1 = 0.8). The expected value for b is equal to the perspective-related myths of nature. We assume that the time lag between planning and actual implementation differs among the management styles. The hierarchistic bureaucratic management style is assumed to have a time lag of five time steps, whereas the egalitarian and individualistic management styles lead to immediate implementation of the cost-benefit analysis. The parameters used to describe the management styles are summarized in Table 1. When the worldview on the dynamics of the lake matches the real dynamics, the assumed parameter values of the perspective lead to an utopia. If not, we call it a dystopia.
Table 1. Assumptions for the implementation of the different lake perspectives.
|
Given q = 8, r = 1, and m = 1, we calculated the effects of implementing each of the three management systems (corresponding to three a priori beliefs about lake dynamics) under simulated conditions that correspond to the three different lake types. The diagonals in Tables 2 and 3 correspond to utopias (where reality matches an agent's expectations), and the off-diagonals correspond to dystopias (where agents are surprised by reality).
Table 2. Utopias and dystopias of the simple formulation of the lake, where input to the lake (L) is the annual phosphorus input from human activities.
| |||||||||||||||||||||
Table 3. Utopias and dystopias of the simple formulation of the lake concerning phosphorus concentration in the lake (P).
| |||||||||||||||||||||
Except for one dystopia, all paths, starting with low inputs (L(0) = 0.1) and a low phosphorus concentration in the water (P(0) = 0.01) lead to an equilibrium. In the egalitarian utopia, low inputs are necessary to remain in an oligotrophic equilibrium. The hierarchistic utopia assumes a somewhat higher input, whereas the individualistic utopia assumes relative high inputs without leading to eutrophication of the lake. Dystopias arise when the implemented management style does not go along with the actual dynamics of nature. Severe eutrophication occurs when individualistic management style is followed, but lake dynamics accord with the egalitarian or hierarchist myths of nature. The same holds for a hierarchist management style and a lake following the dynamics of the egalitarian myth of nature. In terms of the adaptive cycle of Holling, the system flips from an oligotrophic lake into a eutrophic lake. The oscillation, which occurs when an ephemeral lake is managed according to the individualistic management style, is caused by the reaction to limit the very high levels of eutrophication, resulting in high economic costs. All other dystopias result in an oligotrophic lake. This analysis shows that a wrong perception of the system dynamics leads to severe consequences when the system is sensitive (irreversible lake). This is less the case for other type of lakes.
Ecosystems are characterized by different types of dynamics in the time scale and spatial scale (Holling 1992). The simple lake model consists only of fast dynamics; to enhance its realism, we include a slow variable, the mud equation. This equation assumes that phosphorus is sedimented in the mud. A small proportion k (= 0.01) of the phosphorus in the mud is lost each year to permanent burial.
Due to the inclusion of the mud equation, the recycling rate also becomes dependent on the concentration of phosphorus in the mud. The lake model can be formulated now as:
P[t] = (1-s-h) P[t-1] + L[t] + r M[t-1] f(P[t-1])
M[t] = (1-k) M[t-1] + sP[t-1] -r M[t-1] f(P[t-1])
f(P) = Pq / (mq+Pq)
where s is the proportion of P sedimented each year, and h is the proportion of P flushed each year.
The different types of lakes visualized in the myths of nature are now implemented using the parameter values as given below. Note that the proportion of phosphorus that is lost from the water column, s+h, is equal to the b value of the simple lake model:
nature benign (individualistic view): s = 1.0, h = 0.5
nature perverse/tolerant (hierarchistic view): s = 0.5, h = 0.3
nature ephemeral (egalitarian view): s = 0.2, h = 0.1.
We assume that the agents in the model are not aware of this slow variable. In fact, they have incomplete knowledge of the real system. Therefore, they use the same model as before to optimize inputs by cost-benefit analysis.
If the egalitarian management style is implemented, inputs in the lake are low enough to suppress phosphorus recycling. Therefore, the utopia/dystopia equilibria do not differ from the earlier calculations (Tables 4 and 5). The hierarchist utopia leads now to oscillating levels of inputs and phosphorus concentration in the water. Due to careful management, eutrophication is reversed for awhile. However, because the precise dynamics of the lake are not known, the hierarchist cannot manage the lake to a stable situation. If the dynamics of the lake are not according to the view of the hierarchist myth of nature, the lake either reaches a stable oligotropic state (if the lake is benign) or oscillates between two lower input levels due to fast recycling of sediment phosphorus (if the lake is ephemeral).
Table 4. Utopias and dystopias in the mud dynamics are included in the lake model (lake input L).
| |||||||||||||||||||||
Table 5. Utopias and dystopias in the mud dynamics are included in the lake model (phosphorus concentration in the lake, P).
| |||||||||||||||||||||
The individualistic management style causes the lake to become highly eutrophic. In the individualistic utopia, the level of phosphorus in the water reaches a high level, which accelerates recycling.
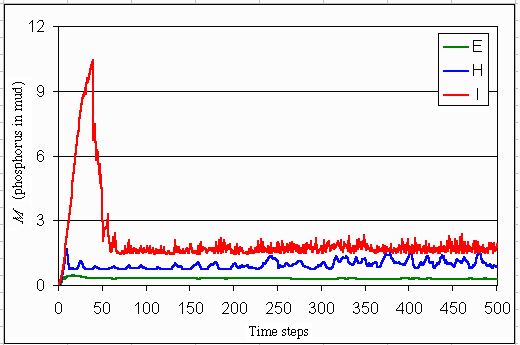
The levels of input (L), phosphorus in the water (P), and sedimented phosphorus (M) are depicted in Figs. 5, 6, and 7. These show the precautionary low level of inputs in the egalitarian utopia, which leads in the long run to a phosphoric time bomb because of the high level of phosphorus in the mud (Fig. 7). A small disturbance in this situation may lead to severe consequences. Thus, it might be concluded that an egalitarian utopia reduces the resilience in this model world. In the hierarchistic utopia, an adaptive cycle appears (Fig. 2). The ignored slow dynamics of sedimentation of phosphorus in mud leads to surprises, which trigger management to reduce inputs. In the individualistic utopia, reactive management leads to a successful control of the lake.
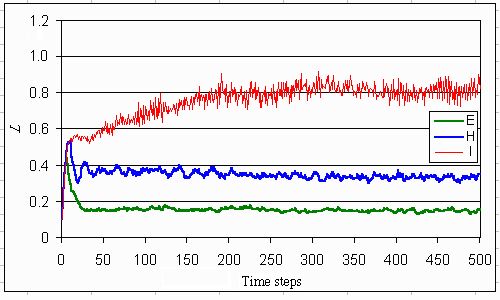
Fig. 5. Input in the water for three utopian cases (E, egalitarian; H, hierarchist; and I, individualist).
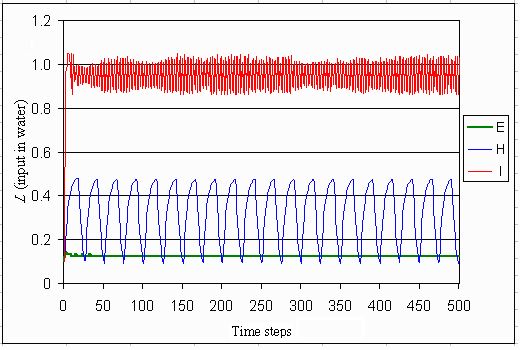
|
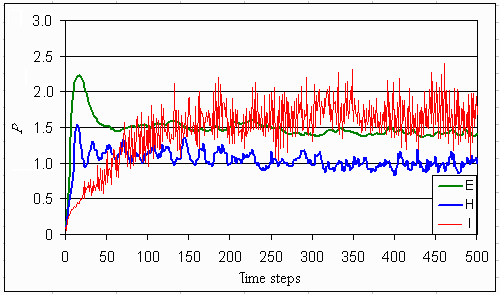
Fig. 6. Concentration of phosphorus in the water for each utopia.
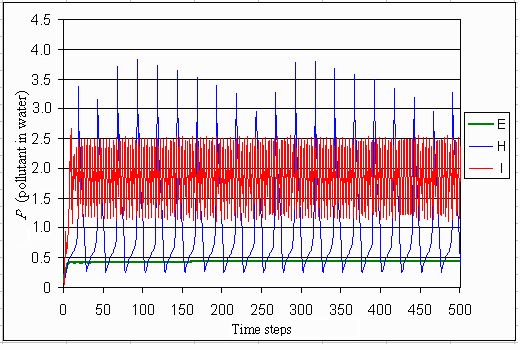
|
Fig. 7. Concentration of phosphorus in the mud for each utopia.
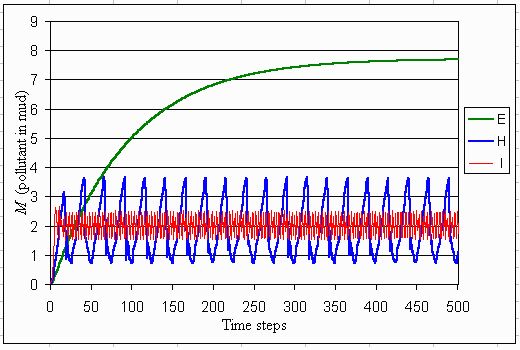
|
Figs. 8, 9, and 10 depict the relationship of the inputs (L) and the estimated value of parameter b in the simple lake model for the three utopias (estimated b = L[t]/P[t -1] + P[t -1](q -1)/(mq + P[t -1]q)). In fact, the parameter b exists only in the models of the agents. Although agents have a fixed expectation of b, the b value of the simple lake can be calculated using the output of the more complex lake model. This enables us to see how well or badly the different perspectives perform. The egalitarian utopia leads to a fast stable point in the irreversible zone of the bifurcation diagram (Fig. 8). The stable point has a b value of about 0.3, as was assumed by the egalitarian. The hierarchist assumes a b value of 0.8, but the calculated b value of the hierarchistic utopia leads to a "butterfly of the lake" (referring to the strange attractor found by Lorenz (1963) in atmospheric models), where the state of the lake cycles through the different zones of lake dynamics. The inputs are increased in every cycle until phosphorus concentration in the water reaches such a high level that damage costs are expected to be too high. Due to the inertia in decision making, the inputs remain to increase somewhat more before it drops to a very low level. This very low level is needed because of the expected damages resulting from the high phosphorus level in the water. The cycle can start again. This shows a successful management according to the dynamics of the Holling cycle. The individualistic utopia results in oscillation in the reversible zone of lake dynamics in the neighborhood of the assumed b value of the individualist.
Fig. 8. Trajectory of the egalitarian utopia in the bifurcation diagram of the simple lake model.
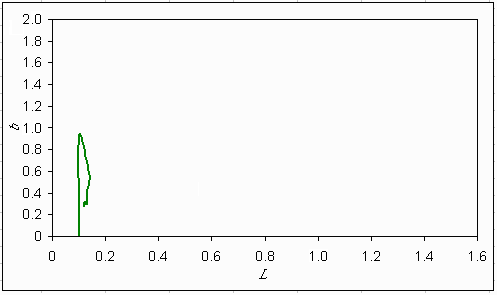
|
Fig. 9. Trajectory of the hierarchistic utopia in the bifurcation diagram of the simple lake model.
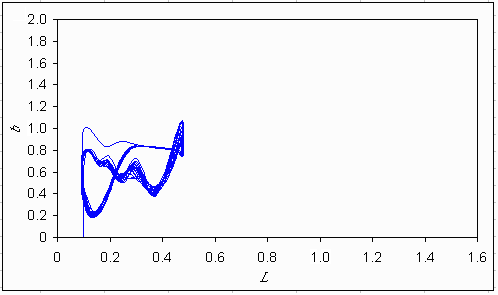
|
Fig. 10. Trajectory of the individualistic utopia in the bifurcation diagram of the simple lake model.
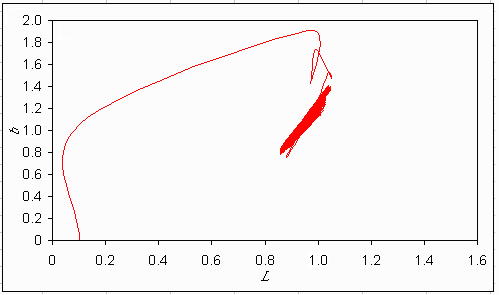
|
The agent managing the lake in the previous sections does not learn from observations about how the real world actually behaves. In case of surprises, the mental model of the lake dynamics is not updated. In this section, we introduce an algorithm, which simulates a kind of learning process. According to Thompson et al. (1990), people are assumed to abandon their perspectives in the event of surprise, that is, if surprises differ from expectations. People who adhere to a certain worldview will switch to another one if it can better explain the observed behavior of the system. Following Janssen and de Vries (1998), this process is simulated by using a genetic algorithm. Genetic algorithms simulate the process of natural selection by considering a population of agents producing offspring who are similar, but not identical, to their parents (Goldberg 1989, Holland 1992, Mitchell 1996). This process depends on three genetic operators: selection, crossover, and mutation. Selection means that the genetic algorithm selects n copies of the strings (genetic code) in the population by a random process that favors the most fit. Subsequently, these copies are probabilistically paired in a mating process whereby each pair produces two offspring by means of crossover and mutation. Crossover means that two offspring are created with a certain probability that the genetic information is crossed over; otherwise, the offspring are identical to the parents. In case of crossover, the parent strings of genetic information are split in a random point and are swapped to shape two new strings. Each element of the genetic information has a small probability of being altered. This mutation is independent of what happens with the other genetic information.
We define a population of 50 agents and distribute management styles among them. The agents compare the observed phosphorus concentration in the water with the expected level. The expected level for the agents' perspective i is given by
Ei{P[t]} = (1-bi)Pobs[t -1] + L[t] +Pobs[t -1]q/(mq+Pobs[t -1]q)
where Pobs[t -1] is the observed phosphorus, and bi is the loss proportion according to the myth of nature of agent i. In the next step, we define a fitness function that is a measure of how well the system behavior for a given management style fits with the real-world observations. Here, the fitness function is a function of the expected phosphorus level in the water and the observed level. The larger the discrepancy between the observed and expected levels, the less fit is the management style with regard to the real lake dynamics. If they totally match, the fitness is maximal (=1):
fitness = 1-{abs(Ei[P] - Pobs)/[0.5 + abs(Ei[P] - Pobs)]}.
The genetic algorithm and the dynamic system model of the lake are integrated in the following manner. Given values for the loss rate b, the discount rate Δ, and the value β1 of the quality assessment of the water function, the dynamic system, calculates the optimal value for the input of phosphorus L. We calculate at each time step the optimal level for each of the three perspectives. The distribution of the perspectives among the population of agents weights the influence, and therefore the actual level of L. For the time being, we assume that the input level L is an equally weighted average among the agents.
Suppose that the lake dynamics are ephemeral and that the agents have, initially, an individualistic management style. Fig. 11 shows that a flip to the eutrophic state leads to a sharp decrease in the average fitness of the agents' perspectives. A more egalitarian management style leads to a reduction of the inputs and a change of the lake into an oligotrophic state (Figs. 12, 13, and 14). Later, the hierarchic management style will dominate the average perspective of the agents. Because the real dynamics of the system are not known (one is unaware of the slow mud dynamics), the average fitness of the perspectives will never reach the maximum value. This example shows that learning can prevent the system from flipping to another state.
Fig. 11. The average fitness of the agents. A value of one means a perfect fit of observations with expectations. This is one single run for an irreversible lake.
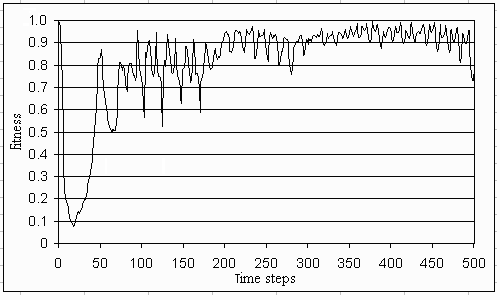
|
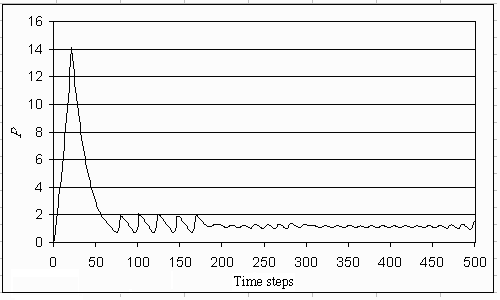
Fig. 13. Input of phosphorus in the lake if the initial perspective is individualistic and the lake dynamics are ephemeral. This is one single run for an irreversible lake.
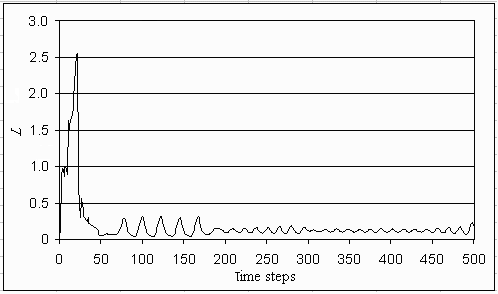
|
Fig. 14. Concentration of phosphorus in the lake if the initial perspective is individualistic and the lake dynamics are ephemeral. This is one single run for an irreversible lake.
|
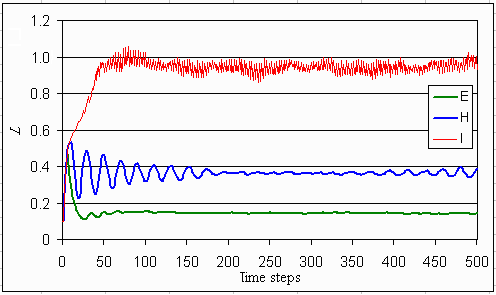
We performed 100 runs with random initial distributions of the agents' perspectives for each type of lake dynamics. The averages are depicted in Figs. 15-20. In all cases, the input increases up to 0.5 during the first 10 time steps. Thereafter, input, in the case of an ephemeral (irreversible) lake, reduces to a stable level under 0.2. In the hierarchist's myth of nature, the inputs fluctuate at a decreasing pulse and reduce to a level around 0.5. In the case of a reversible lake, the input fluctuates around 1.0.
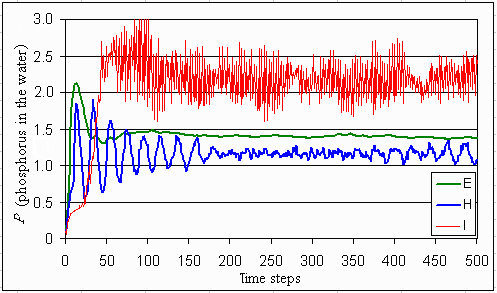
Fig. 16. Expected concentration of phosphorus in the water if the dynamics of the lake are according to one of the three myths of nature.
|
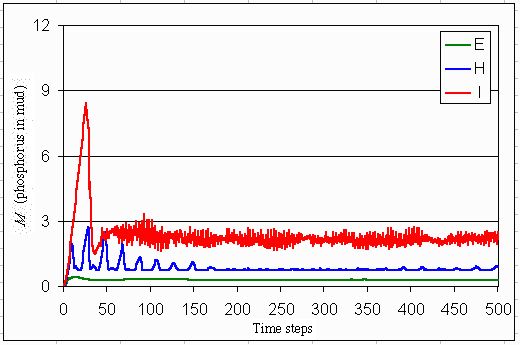
Fig. 17. Expected concentration of phosphorus in the mud if the dynamics of the lake are according to one of the three myths of nature.
|
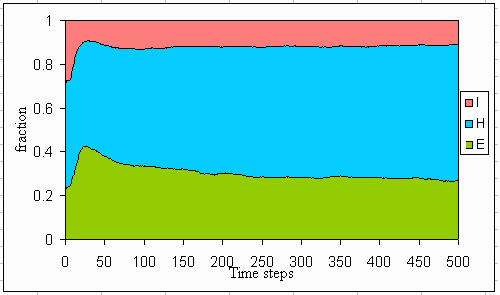
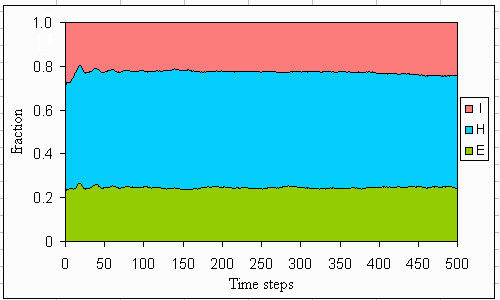
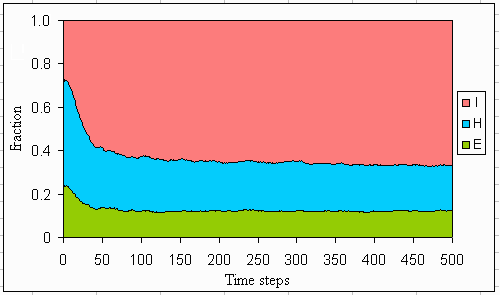
Phosphorus concentrations in the lake do not differ very much between the myths of nature: all are eutrophic. In the individualistic and hierarchistic worldview, this is not a real problem as long as the level of phosphorus is controlled such that it balances economic costs and benefits. In the egalitarian case, with an ephemeral lake, eutrophication can only be prevented in the utopian case (see Figs. 5-7). The phosphorus in the mud stabilizes at various levels. This level is somewhat higher for the reversible lake than for the utopian case. However, the level is now much lower for the irreversible lake than for the utopian case, where a kind of phosphorus time bomb has built up. Figs. 18-20 show that a mix of all three perspectives remains, although the agents learn and adapt. Because the dynamics of the lake do not follow one of the myths of nature, such a mix is necessary to maintain lake resilience.
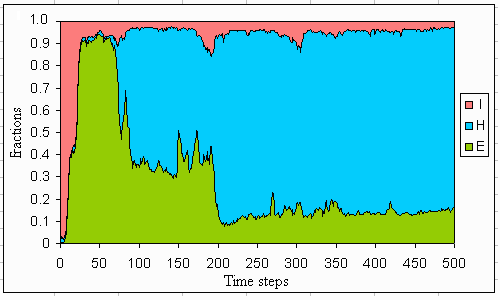
Fig. 18. Average distribution of perspectives if the lake dynamics are ephemeral.
|
Fig. 19. Average distribution of perspectives if the lake dynamics are stable within limits.
|
Fig. 20. Average distribution of perspectives if the lake dynamics are benign.
|
Stochastic inputs
Nonpoint inputs such as those from agricultural activities are highly variable in time (Lathrop et al. 1998). We include this variability by adding a stochastic term exp(sf*z) where z is a random variable from a Student's t distribution, using 10 degrees of freedom, and sf is a scaling factor (0.2 in our calculations).
P[t] = (1-s-h) P[t-1] +exp(sf*z) * L[t] + r M[t-1] f(P[t-1]).
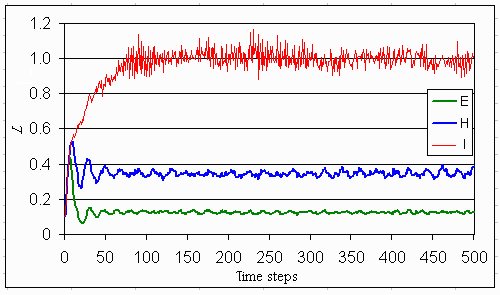
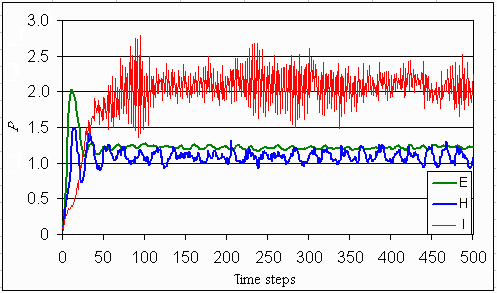
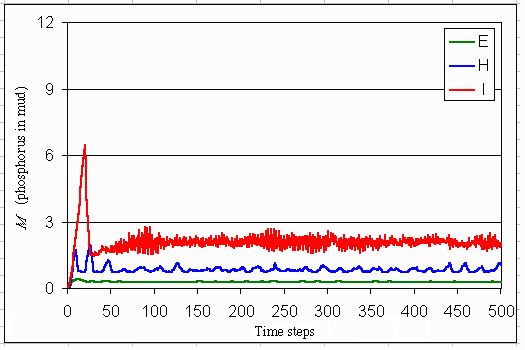
Stochasticity does not change the average state of the system (Figs. 21-23). Stochasticity dampens the oscillating inputs when the lake dynamics are stable within limits (hierarchistic worldview), because stochastic events make the agents aware sooner of the limits of the system's stability domain. The stochastic fluctuations, combined with faster learning, lead to a reduction of phosphorus levels in the mud.
Fig. 21. Expected input in the lake if the dynamics of the lake are according to one of the three myths of nature and if the inputs are confronted with stochastic disturbances.
|
Fig. 22. Expected phosphorus concentration in water if the dynamics of the lake are according to one of the three myths of nature and if the inputs are confronted with stochastic disturbances.
|
Fig. 23. Expected phosphorus concentration in the mud if the dynamics of the lake are according to one of the three myths of nature and if the inputs are confronted with stochastic disturbances.
|
Ignorance
So far, we have been rather optimistic about the ability of agents to learn and adapt. It might be more realistic to introduce some ignorance. This means that small mismatches between observations and expectations do not lead to changes in worldview. Let the variable eps represent the smallest detectable error. That is, if the mismatch is smaller than eps, the fitness is maximal.
If abs(Ei[P]-Pobs) eps, then fitness = 1
such that
if Ei[P]>Pobs+eps, then fitness = 1-{Ei[P]-Pobs-eps)/[0.5+(Ei[P]-Pobs-eps)]}.
If Ei[P]<Pobs-eps, then fitness = 1-{(Pobs-Ei[P]-eps)/[0.5+(Pobs-Ei[P]-eps)]}.
Ignorance leads to delay in learning (Figs. 24-26). Only significant surprises lead to changes in perspectives. It is therefore no surprise that the lake inputs become closer to each other for the three different types of lake dynamics. The inputs in the case of a reversible lake become lower, whereas those inputs in the case of an irreversible lake are slightly higher. This leads to similar lake states for different types of dynamics. Because of a delay in leading, the phosphorus level in the mud reaches high levels for a short period (Fig. 26).
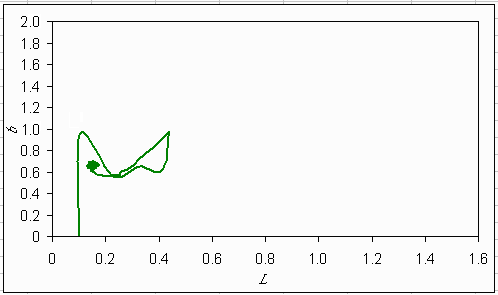
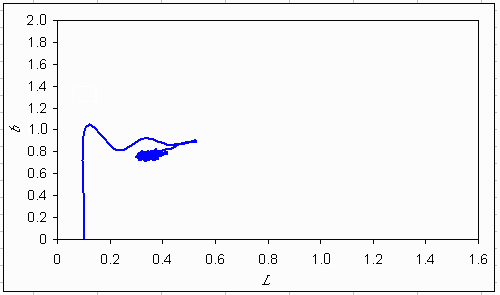
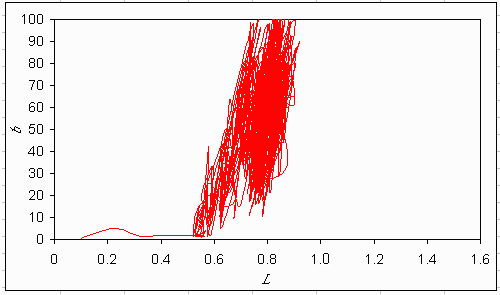
The learning process can also be visualized by the bifurcation diagrams (Figs. 27-29). For the irreversible and hysteretic lake, the agents converge to a point in the bifurcation diagram. For the reversible lake, the agents remain wandering around, reacting to stochastic events.
Fig. 27. Trajectory of learning agents in the bifurcation diagram if the lake dynamics are ephemeral.
|
Fig. 28. Trajectory of learning agents in the bifurcation diagram if the lake dynamics are stable within limits.
|
Fig. 29. Trajectory of learning agents in the bifurcation diagram if the lake dynamics are benign.
|
In this paper, we have developed and analyzed an integrated model for lake management in which agents respond to unexpected changes in the state of the lake. Our goal has been to use a caricature of social decision making for a nonlinear, fast-slow ecosystem to explore some aspects of sustainability. Many features of this model could be caricatured in different ways. For example, the structural model used to assess the state of the lake, the parameter choices used to characterize the perspectives, and the genetic algorithm used to propagate the perspectives are all choices from a spectrum of alternatives. Within the Resilience Network, a set of models of human-nature interactions is developed. The model discussed in this paper focuses on the agents' myths of nature; other models focus on social interaction, institutions, stochastic optimization, and so on. More integration of these different approaches and more empirical studies are needed in future. We suggest that our results justify a careful, thorough exploration of diverse models.
We have distinguished three types of lakes: reversible, hysteretic, and irreversible. Agents are assumed to have limited knowledge about the lake dynamics. Comparing the different utopias, we can conclude that egalitarians prefer a very low input of phosphorus, hierarchists prefer an adaptive management style leading to a cycle of input values, and individualists prefer a high input of phosphorus to derive economic output. In the case of a preventive management style (egalitarian) applied to an ephemeral lake, phosphorus concentration remains low in the water, but the level of phosphorus in the mud increases, creating a time bomb. Only a small disturbance in the input may lead to catastrophic phosphorus levels in the lake. The preventive management style reduces the resilience of the ephemeral lake. The egalitarian utopia case is therefore a self-fulfilling prophecy. Note that another management style than the preventive one leads to a high level of eutrophication in an irreversible lake.
In the case of a command-and-control management style (hierarchist) applied to a lake that is stable within limits, the lake goes through all possible states. The resulting "butterfly of the lake" illustrates the adaptive cycle of Holling (1986). A reactive individual management style applied to a lake with reversible dynamics leads to relative high inputs without much disturbance to the lake's state.
If agents learn and adapt to unexpected changes in the state of the lake, a mix of perspectives is preferred to manage the resilience of the system. Although low levels of phosphorus in the lake will not be reached, the lake is prevented from flipping to catastrophically high phosphorus levels because of the limited buildup of phosphorus in the mud. This conclusion also holds if we introduce stochastic events and ignorance to small changes in the state of the lake.
In the model, the agents are always learning, but never get it exactly right. They come close enough, however, to sustain the social and ecological system. Despite imperfect learning, adaptive management maintains the resilience.
Responses to this article are invited. If accepted for publication, your response will be hyperlinked to the article. To submit a comment, follow this link. To read comments already accepted, follow this link.
This paper was supported by the Resilience Network and was inspired by the meeting on Malta in April 1998. Thanks to Rusty Pritchard and four anonymous reviewers for the many constructive comments on an earlier version of this paper.
Blaikie, P., and H. Brookfield. 1987. Land degradation and society. Methuen, London, UK.
Carpenter, S. R., W. A. Brock, and P. C. Hanson. 1999b. Complex dynamics from simple interactions of people and ecosystems. Conservation Ecology 3
Carpenter, S. R., J. J. Cole, J. F. Kitchell, and M. L. Pace. 1998. Impact of dissolved organic carbon, phosphorus and grazing on phytoplankton biomass and production in experimental lakes. Limnology and Oceanography 43:73-80.
Carpenter, S. R., D. Ludwig, and W. A. Brock. 1999a. Management of eutrophication for lakes subject to potentially irreversible change. Ecological Applications 9:751-771.
Cooke, G. B., E. B. Welch, S. A. Peterson, and P. R. Newroth. 1993. Restoration and management of lakes and reservoirs. Lewis Publishers, Boca Raton, Florida, USA.
Goldberg, D. 1989. Genetic algorithms in search, optimization, and machine learning. Addison-Wesley, Reading, Massachusetts, USA.
Holland, J. H. 1992. Genetic algorithms. Scientific American 267: 44-50.
Holling, C. S. 1978. The spruce-budworm/forest-management problem. Pages 143-182 in C. S. Holling, editor. Adaptive environmental assessment and management. John Wiley, New York, New York, USA.
Holling, C. S. 1986. The resilience of terrestrial ecosystems: local surprise and global change. Pages 292-317 in W. C. Clark and R. E. Munn, editors. Sustainable development of the biosphere. Cambridge University Press, Cambridge, UK.
Holling, C. S. 1992. Cross-scale morphology, geometry, and dynamics of ecosystems. Ecological Monographs 62:447-502.
Holling, C. S. 1994. An ecologist's view of the Malthusian conflict. Pages 79-103 in K. Lindahl-Kiessling and H. Landberg, editors. Population, economic development, and the environment. Oxford University Press, New York, New York, USA.
Holling, C. S., L. H. Gunderson, and G. D. Peterson. In press. In quest of a theory of adaptive change. In L. H. Gunderson, C. S. Holling, and G. D. Peterson, editors. Theories for sustainable futures: understanding and managing for resilience in human-ecological systems.
Janssen, M. A. 1998. Modelling global change: The art of integrated assessment modelling. Edward Elgar Publishers, Cheltenham, UK/ Northampton, Massachusetts, USA.
Janssen, M. A., and H. J. M. de Vries. 1998. The battle of perspectives: a multi-agents model with adaptive responses to climate change. Ecological Economics 26: 43-65.
Larson, D. P., D. W. Schults, and K. Malueg. 1981. Summer internal phosphorus supplies on Shagawa Lake, Minnesota. Limnology and Oceanography 26: 740-753.
Larson, D. P., J. van Sickel, K. W. Malueg, and D. P. Smith. 1979. The effect of wastewater phosphorus removal on Shagawa Lak, Mennesota: Phosphorus supplies, lake phosphorus and chlorophyll a. Water Research 13: 1259-1272.
Lathrop, R. C., S. R. Carpenter, C. A. Stow, P. A. Soranno, and J. C. Panuska. 1998. Phosphorus loading reductions needed to control flue-green algal blooms in Lake Mendota. Canadian Journal of Fisheries and Aquatic Sciences 55(5):1169-1178.
Lorenz, E. N. 1963. Deterministic non-periodic flow. Journal of the Atmospheric Sciences 20:130-141.
Mitchell, M. 1996. An introduction to genetic algorithms. Cambridge MIT Press, Cambridge, Massachusetts, USA.
Nurnberg, G. K. 1984. Prediction of internal phosphorus load in lakes with anoxic hypolimnia. Limnology and Oceanography 29:135-145.
Odum, E. P. 1997. Ecology: A bridge between science and society. Sinauer Associates, Sunderland, Massachusetts, USA.
Price, M. F., and M. Thompson. 1997. The complex life: human land uses in mountain ecosystems. Global Ecology and Biogeography Letters 6:77-90.
Rayner, S. 1991. A cultural perspective on the structure and implementation of global environmental agreements. Evaluation Review15(1):75-102.
Sas, H. 1989. Lake restoration by reduction of nutrient loading: Expectations, experiences, extrapolations. Academia Verlag, Richarz, St. Augustin.
Scheffer, M., H. Hosper, M.-L. Meijer, B. Moss, and E. Jeppesen. 1993. Alternative equilibia in shallow lakes. Trends in Ecology and Evolution 8:275-279.
Schindler, D. W. 1977. Evolution of phosphorus limitation in lakes. Science 195:260-262.
Schindler, D. W., R. H. Hesslein, and M. A. Turner. 1987. Exchange of nutrients between sediments and water after15 years of experimental eutrophication. Canadian Journal of Fisheries and Aquatic Sciences 44:26-33.
Schwartz, M., and M. Thompson. 1990. Divided we stand: Redefining politics, technology, and social choice. Harvester Wheatsheaf, New York, New York, USA.
Smith, V. H. 1998. Cultural eutrophication of inland, estuarine and coastal waters. Pages 7-49 in M. L. Pace and P. M. Groffman, editors. Successes, limitations and frontiers of Ecosystem Science. Springer-Verlag, New York, New York, USA.
Soranno, P. A., S. R. Carpenter, and R. C. Lathrop. 1997. Internal phosphorus loading in Lake Mendota: response to external loads and weather. Canadian Journal of Fisheries and Aquatic Sciences 54:1883-1893.
Thompson, M., R. Ellis, and A. Wildawsky. 1990. Cultural theory. Westview Press, Boulder, Colorado, USA.
Wilson, M. A., and S. R. Carpenter. 1999. Economic valuation of freshwater ecosystem services in the United States, 1977-1997. Ecological Applications 9:772-783.
This self-extracting zipfile contains a demo version of the model. See the readme file for
information.